阅读提示:
如果是移动端阅读,可能会发生公式截断的问题,需要将设备横屏变为宽屏模式才能正常阅读.毕竟数学内容不同于纯文字.
另外,网站采用mathjax渲染latex代码,qq或者微信内置浏览器第一次打开可能会只显示源码不作处理.需要退出后再次打开才能正确渲染,其他浏览器应无问题.
如图,在锐角$\triangle ABC$中,$AB>AC$,$M$是$\triangle ABC$的外接圆$\Omega$的劣弧$BC$的中点,$K$是$\angle BAC$的外角平分线与$BC$延长线的交点.在过点$A$且垂直于$BC$的直线上取一点$D$(异于$A$),使得$DM=AM$.设$\triangle ADK$的外接圆与圆$\Omega$相交于点$A$及另一点$T$.证明:$AT$平分线段$BC$
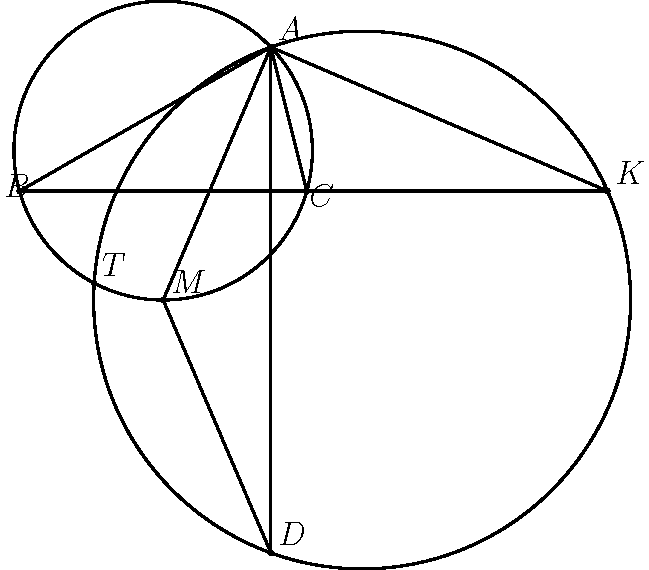
显然$T$的位置不太清楚,但$AT$是根轴是明确的,所以可以直接取出$BC$中点$F$,证明$F$在根轴上.也就是证明$F$对两个圆的幂是相等的.
等等,这不就是今年A1的套路吗?这A2真就和A1这么像都不改的?
$F$对$\bigodot ABC$的幂是$\ds \frac{a^2}{4}$,设$\bigodot ADK$交$BC$于不同于$K$的$E$,只需证明$\ds FE \cdot FK=\frac{a^2}{4}$
考虑外角平分线基本性质$\ds \frac{KB}{KC}=\frac{c}{b}$,可得$\ds KC=\frac{ab}{c-b}$,$\ds KF=\frac{a}{2}+KC=\frac{a(c+b)}{2(c-b)}$
从而只需证明$\ds FE=\frac{a^2}{4}/\frac{a(c+b)}{2(c-b)}=\frac{a(c-b)}{2(c+b)}$
只需证明$\ds CE=FE+\frac{a}{2}=\frac{ac}{c+b}$
可这就是角平分线分割$BC$的两段长度之一,设$AM$交$BC$于$G$,只需证明$BG=CE$,只需证明$MG=ME$,考虑这边还有一个等腰三角形$MA=MD$,只需证明$E,M,D$共线即可
稍微导下角发现就没了

设$\triangle ABC$三边为$a,b,c$,$\bigodot ADK$交$BC$于不同于$K$的$E$,$BC$中点$F$,$AM$交$BC$于$G$.
则有$MF \perp BC$.
考虑$\angle EDA=\angle EKA$(共圆),$\angle EKA=90^\circ-\angle AGK=\angle GAD=\angle MDA$
可得$\angle EDA=\angle MDA$,所以$EMD$三点共线
可得$\angle MEG=\angle MGE=90^\circ-\angle MAD,ME=MG$
由对称性,$\ds CE=BG=\frac{ac}{c+b},FE=CE-\frac{a}{2}=\frac{a(c-b)}{2(c+b)}$
又由外角平分线基本性质$\ds \frac{KB}{KC}=\frac{c}{b}$,可得$\ds KC=\frac{ab}{c-b}$,$\ds FK=\frac{a}{2}+KC=\frac{a(c+b)}{2(c-b)}$
从而$\ds FK \cdot FE=\frac{a(c+b)}{2(c-b)}\frac{a(c-b)}{2(c+b)}=\frac{a^2}{4}=FB \cdot FC$
故$F$在$\bigodot ABC$和$\bigodot ADK$根轴上,即$F$在$AT$上,证毕.
