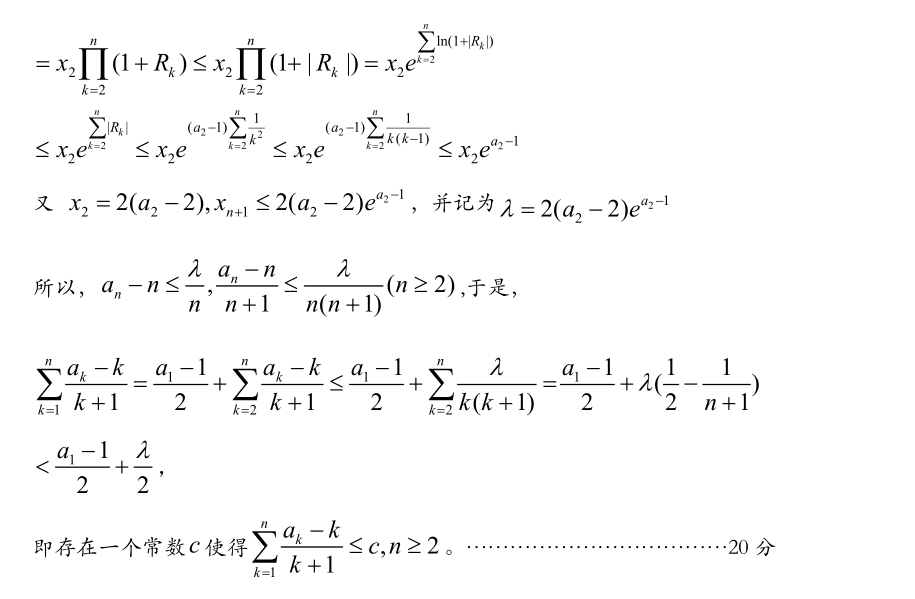参考答案简直丑陋.给个简单解法.
14. 设数列 $\left\{a_{n}\right\}$ 满足 $\ds a_{1}>0, a_{n+1}=a_{n}+\frac{n}{a_{n}}(n \geq 1)$, 证明
(1).数列 $\left\{a_{n}-n\right\}(n \geq 2)$ 为单调递减;
(2).存在一个常数 $c$ 使得 $\ds \sum_{k=1}^{n} \frac{a_{k}-k}{k+1} \leq c, n \geq 2$ 。
(1). 归纳证$a_n \ge n,\forall n \ge 2$,然后可得$\ds a_{n+1}-(n+1)=(1-\frac{1}{a_n})(a_n-n)<a_n-n$
(2).由(1)可知,当$n \ge 2$时$a_{n}-n\le a_2-2$
取$\lambda=\max\{1,a_2-2\}$,则$a_n \le n+(a_2-2)\le \lambda (n+1)$ \[ (a_k-k)-(a_{k+1}-(k+1))=\frac{a_k-k}{a_k} \ge \frac{a_k-k}{\lambda (k+1)} \]
累加可得 \[ \sum_{k=2}^n \frac{a_k-k}{k+1} \le \lambda[(a_2-2)-(a_{n+1}-(n+1))] \le \lambda (a_2-2) \]
从而 \[ \sum_{k=1}^{n} \frac{a_{k}-k}{k+1} \le \frac{a_1-1}{2}+\lambda (a_2-2) \]
因此,取$\ds c=\frac{a_1-1}{2}+\lambda (a_2-2)$即可
参考答案如下: