阅读提示:
如果是移动端阅读,可能会发生公式截断的问题,需要将设备横屏变为宽屏模式才能正常阅读.毕竟数学内容不同于纯文字.
另外,网站采用mathjax渲染latex代码,qq或者微信内置浏览器第一次打开可能会只显示源码不作处理.需要退出后再次打开才能正确渲染,其他浏览器应无问题.
P4.给定非等边$\triangle ABC$,记其内心为$I$,内切圆分别切三边$BC$、$CA$、$AB$于$D$、$E$、$F$.令$P$为$AI$与$DF$的交点,$Q$为$BI$与$EF$的交点.证明:$PQ=CD$.
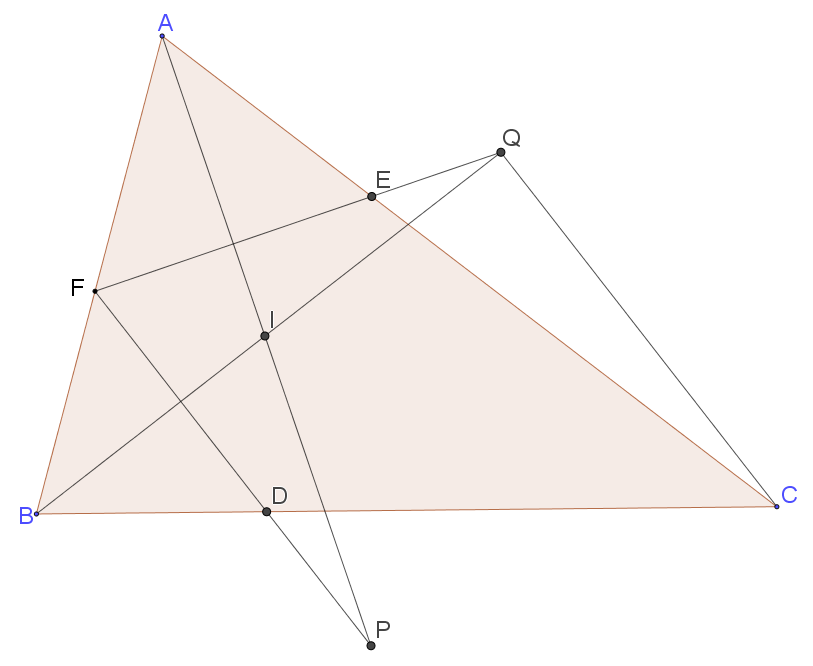
解析:观察$PQ,CD$,可以猜测$PDQC$应该是个等腰梯形,而$Q$在$DF$中垂线上,所以应该有$FQCP$是平行四边形.到这里就应该想到一个引理了(但是这个引理文字叙述起来非常拗口).
大约是12年的IMO考过,后面东南女奥也考过几回.
对于本题而言,就是$Q$为$C$在$BI$上的垂足,$P$为$C$在$AI$上的垂足.而后稍微导一导就行了.
证明:$\angle FQB=\angle AFE-\angle ABI=90^\circ-\frac{A}{2}-\frac{B}{2}=\frac{C}{2}=\angle ACI$
故$EQCI$共圆,$\angle IQC=\angle IEC=90^\circ$
考虑$DF \perp BQ$,于是$CQ//DF$
同理$\angle CPI=90^\circ$(这其实意味着$IEQCPD$六点共圆),及$CP//EF$,于是$FQCP$是平行四边形.
结合$QD=QF$就有$PDQC$是等腰梯形,对角线$PQ=CD$
