设 $H, O$ 分别为非等边锐角三角形 $A B C$ 的垂心和外心, 设 $C$ 关于直线 $A B$ 的对称点为 $C^{\prime}, B C^{\prime} \cap A O=L$, 过 $B$ 作关于 $A O$ 的平行线交直线 $A C$ 于点 $Z$, 求证: $\angle L Z B=\angle C Z H$.
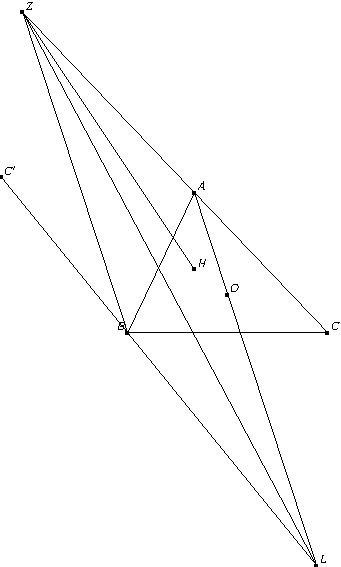
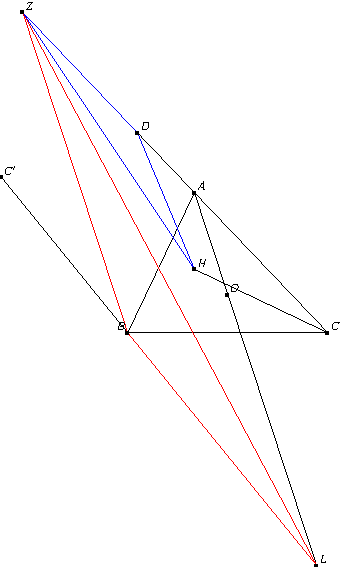
解析:容易得$\angle ZBL=90^\circ+A$,结合$\angle HCA=90^\circ-A$,所以我们可以尝试强行构造相似三角形,用SAS的方式证明相似从而得等角.具体如下
以$H$为圆心,$HC$为半径作圆,交$ZC$于不同于$C$的点$D$,则$\angle ZDH=\angle ZBL=90^\circ+A$
我们只需证明$\frac{DZ}{DH}=\frac{BZ}{BL}$即可证明原题
\begin{align} \frac{BZ}{BL}&=\frac{BZ}{BA}\frac{BA}{BL}\\ &=\frac{\sin A}{\cos B}\frac{\cos A}{\cos C} \end{align}
另一方面,考虑$CD=2CH \cdot \cos\angle ACH=2CH\sin A$,以及 \begin{align} \frac{CZ}{CH}&=\frac{CA+AZ}{AB}\frac{AB}{CH}\\ &=(\frac{CA}{AB}+\frac{AZ}{AB})\frac{AB}{CH}\\ &=(\frac{\sin B}{\sin C}+\frac{\cos C}{\cos B})\frac{\sin C}{\cos C}\\ &=\frac{\sin 2B+\sin 2C}{2\cos B \cos C}\\ &=\frac{\sin(B+C)\cos(B-C)}{\cos B \cos C}\\ &=\sin A \frac{\cos(B-C)}{\cos B \cos C} \end{align}
所以 \begin{align} \frac{DZ}{DH}&=\frac{CZ-2CH\sin A}{DH}=\frac{CZ}{CH}-2\sin A\\ &=\sin A \frac{\cos(B-C)}{\cos B \cos C}-2\sin A\\ &=\sin A \frac{\cos(B-C)-2\cos B \cos C}{\cos B \cos C}\\ &=\sin A \frac{-\cos(B+C)}{\cos B \cos C}\\ &=\frac{\sin A \cos A}{\cos B \cos C}=\frac{BZ}{BL} \end{align}
证毕.
