设 $H, O$ 分别为非等边锐角三角形 $A B C$ 的垂心和外心, 设 $C$ 关于直线 $A B$ 的对称点为 $C^{\prime}, B C^{\prime} \cap A O=L$, 过 $B$ 作关于 $A O$ 的平行线交直线 $A C$ 于点 $Z$, 求证: $\angle L Z B=\angle C Z H$.

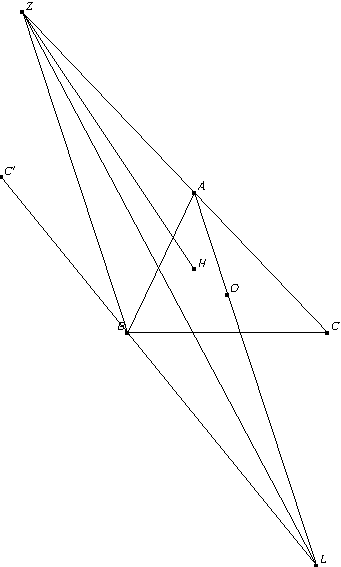
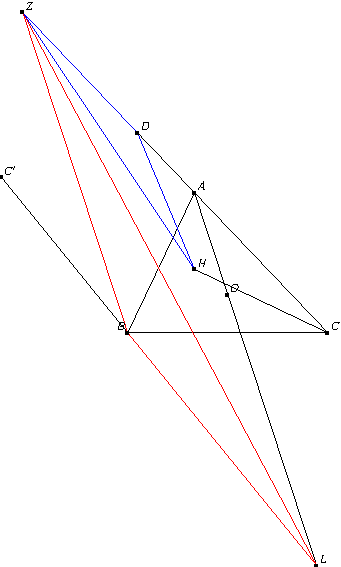
解析:容易得$\angle ZBL=90^\circ+A$,结合$\angle HCA=90^\circ-A$,所以我们可以尝试强行构造相似三角形,用SAS的方式证明相似从而得等角.具体如下
    以$H$为圆心,$HC$为半径作圆,交$ZC$于不同于$C$的点$D$,则$\angle ZDH=\angle ZBL=90^\circ+A$
    我们只需证明$\frac{DZ}{DH}=\frac{BZ}{BL}$即可证明原题
    \begin{align}        \frac{BZ}{BL}&=\frac{BZ}{BA}\frac{BA}{BL}\\        &=\frac{\sin A}{\cos B}\frac{\cos A}{\cos C}    \end{align}
    另一方面,考虑$CD=2CH \cdot \cos\angle ACH=2CH\sin A$,以及    \begin{align}        \frac{CZ}{CH}&=\frac{CA+AZ}{AB}\frac{AB}{CH}\\        &=(\frac{CA}{AB}+\frac{AZ}{AB})\frac{AB}{CH}\\        &=(\frac{\sin B}{\sin C}+\frac{\cos C}{\cos B})\frac{\sin C}{\cos C}\\        &=\frac{\sin 2B+\sin 2C}{2\cos B \cos C}\\        &=\frac{\sin(B+C)\cos(B-C)}{\cos B \cos C}\\        &=\sin A \frac{\cos(B-C)}{\cos B \cos C}    \end{align}
    所以    \begin{align}        \frac{DZ}{DH}&=\frac{CZ-2CH\sin A}{DH}=\frac{CZ}{CH}-2\sin A\\        &=\sin A \frac{\cos(B-C)}{\cos B \cos C}-2\sin A\\        &=\sin A \frac{\cos(B-C)-2\cos B \cos C}{\cos B \cos C}\\        &=\sin A \frac{-\cos(B+C)}{\cos B \cos C}\\        &=\frac{\sin A \cos A}{\cos B \cos C}=\frac{BZ}{BL}    \end{align}
    证毕.

2023中国TST测试3第4题

4. 如图, 圆 $\Gamma, \Gamma_1, \Gamma_2$ 两两外切, 且均与直线 $l$ 相切. 设 $\Gamma, \Gamma_1$ 切于点 $B_1, \Gamma, \Gamma_2$ 切于 点 $B_2, \Gamma_1, \Gamma_2$ 切于点$C$. $\Gamma, \Gamma_1, \Gamma_2$ 分别与 $l$ 切于点 $A, A_1, A_2$, 其中 $A$ 在线段 $A_1 A_2$ 上. 设直 线 $A_1 C, A_2 B_2$ 交于点 $D_1$, 直线 $A_2 C, A_1 B_1$ 交于点 $D_2$. 求证: $D_1 D_2 / / l$.

解析:本题初看圆很多很复杂,但是略加分析会发现其中大部分长度都是可表示的.这会提示我们用计算法.(实际上如果给定$\Gamma$的话,$\Gamma_1,\Gamma_2$的圆心在同一个定抛物线上).

    设$\Gamma,\Gamma_1,\Gamma_2$的圆心分别为$O,O_1,O_2$,半径分别为$1,r,R$.$AA_1=2x,AA_2=2y$,不妨设$x<y$
    则对$O_1 O A A_1$使用勾股定理(省略垂线那一步)可得    \[        (r+1)^2=(r-1)^2+(2x)^2,r=x^2        \]        同理$R=y^2$
    再对$O_1 O_2 A_2 A_1$使用勾股定理    \[        (R+r)^2=(R-r)^2+(2x+2y)^2        \]        解得    \[        4(x+y)^2=4Rr=4x^2 y^2,x+y=xy        \]        到这里为止,我们找到了三个圆的全部限制.由于表达式非常友好(整式多项式),就算暴力手段也是可以接受的.但是我们仍然想要尽可能的简化计算.

一开始我考虑计算($[XYZ]$表示$\triangle XYZ$的面积)    \[        \frac{[A_1 B_1 C]}{[A_1 B_1 A_2]}=\frac{[A_2 B_2 C]}{[A_2 B_2 A_1]}        \]        这样可以得到$\frac{CD_2}{D_2 A_2}=\frac{CD_1}{D_1 A_1}$,就完成了证明.但是尝试之后发现计算还是复杂了些.

最终转而证明$A_1 B_1 \cap A_2 B_2$在$C$和$A_1 A_2$中点的连线上.这样配合塞瓦就能证明$D_1 D_2 // l$了
    设$A_1 B_1 \cap A_2 B_2=X$,$A_1 A_2$中点为$Y$.
    基本性质:$\angle A_1 B_1 A=\angle A_2 B_2 A=\angle A_1 C A_2=90^\circ$(作公切线,或者导弦切角) 
    所以$A B_1 X B_2$共圆,也就是说$AX$是$\Gamma$的直径.$AX \perp l,AX=2$
由$AY=y-x$可得,    \[        \tan AYX=\frac{AX}{AY}=\frac{2}{y-x}        \]        由于$CY$是$\Gamma_1,\Gamma_2$公切线,所以$\angle AYC=\angle A_2 O_2 C=2\angle A_2 O_2 Y$
考虑到$xy=x+y$    \[        \tan \angle A_2 O_2 Y=\frac{A_2 Y}{A_2 O_2}=\frac{x+y}{y^2}=\frac{x}{y}        \]
进而    \[        \tan AYC=\tan 2\angle A_2 O_2 Y=\frac{2 \cdot \frac{x}{y}}{1-\left(\frac{x}{y}\right)^2}=\frac{2xy}{(y-x)(y+x)}=\frac{2}{y-x}        \]
这表明$\angle AYC=\angle AYX$,$C,X,Y$三点共线
由塞瓦定理    \[        \frac{CD_2}{D_2 A_2}\frac{A_2 Y}{YA_1}\frac{A_1 D_1}{D_1 C}=1        \]
    \[        \frac{CD_2}{D_2 A_2}=\frac{C D_1}{D_1 A}        \]        所以$D_1 D_2 //l$

    最终我们并没有采用纯粹的计算法,用的是计算和几何性质结合的方式.就难度来说,大概在联赛第2题?从联赛到冬令营到集训队测试,好像没感觉几何题难度有太多上升….

锐角三角形$ABC$中，$D,E,F$为$BC，AC,AB$中点，$X,Y$为$D$在$AB$,$AC$上垂足，过$F$且与$XY$平行的直线与$DY$交于$P$。求证：$AD \perp EP$。

需要知道面积与定比分点的公式

注意到$AD \perp EP \iff$ $E$是$\triangle APD$垂心
\begin{gather}    AD \perp EP \iff AP \perp DE \iff AP //XD \\    \iff [PDX]=[ADX] \iff [FYX]+[DYX]=[ADX] \\    \iff \frac{1}{2}([XAY]-[XBY])+\frac{1}{2}([BXY]+[CXY])=[ADX]\\    \iff \frac{1}{2}([XAY]+[XCY])=[ADX]\end{gather}考虑到\[    [XAY]+[XCY]=[ACX]=2[ADX]    \]结论显然成立

P4.给定非等边$\triangle ABC$,记其内心为$I$,内切圆分别切三边$BC$、$CA$、$AB$于$D$、$E$、$F$.令$P$为$AI$与$DF$的交点,$Q$为$BI$与$EF$的交点.证明:$PQ=CD$.

解析:观察$PQ,CD$,可以猜测$PDQC$应该是个等腰梯形,而$Q$在$DF$中垂线上,所以应该有$FQCP$是平行四边形.到这里就应该想到一个引理了(但是这个引理文字叙述起来非常拗口).
大约是12年的IMO考过,后面东南女奥也考过几回.
对于本题而言,就是$Q$为$C$在$BI$上的垂足,$P$为$C$在$AI$上的垂足.而后稍微导一导就行了.

证明:$\angle FQB=\angle AFE-\angle ABI=90^\circ-\frac{A}{2}-\frac{B}{2}=\frac{C}{2}=\angle ACI$
故$EQCI$共圆,$\angle IQC=\angle IEC=90^\circ$
考虑$DF \perp BQ$,于是$CQ//DF$
同理$\angle CPI=90^\circ$(这其实意味着$IEQCPD$六点共圆),及$CP//EF$,于是$FQCP$是平行四边形.
结合$QD=QF$就有$PDQC$是等腰梯形,对角线$PQ=CD$

在三角形 $A B C$ 中, $A B>A C, I$ 是内心， $A M$ 是中线. 设过 $I$ 且与 $B C$ 垂直的直线与 $A M$ 交于点 $L, I$ 关于点 $A$ 的对称点为 $J$. 证明: $\angle A B J=\angle L B I$.

证明:

    作$ID \perp BC$于$D$,$LE \perp BI$于$E$,延长$BA$至$F$,使得$AF=AB$
    则$LBDE$共圆,$\angle LBI=\angle LDE$;$JFIB$是平行四边形.
    由平行四边形及正弦定理    \begin{gather}        \frac{FJ}{FB}=\frac{IB}{2AB}\\        =\frac{\sin\frac{A}{2}}{2\sin(90^\circ+\frac{C}{2})}=\frac{\sin\frac{A}{2}}{2\cos\frac{C}{2}}    \end{gather}
    显然$$\frac{LE}{LD}=\frac{LI \cos\frac{B}{2}}{LD}=\frac{LI}{LD}\cos\frac{B}{2}$$
    记$BC$边上的高为$h$,外接圆半径$R$,由面积关系    \begin{gather}        \frac{LI}{LD}        =\frac{[AIM]}{[ADM]}=\frac{\frac{1}{2}([AIC]-[AIB])}{\frac{1}{2}([ADC]-[ADB])}\\        =\frac{\frac{r}{2}(b-c)}{\frac{h}{2}(DC-DB)}=\frac{\frac{r}{2}(b-c)}{\frac{h}{2}(b-c)}\\        =\frac{r}{h}=\frac{4R\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}}{2R\sin B \sin C}        =\frac{\sin\frac{A}{2}}{2\cos\frac{B}{2}\cos\frac{C}{2}}    \end{gather}
    故    \[        \frac{LE}{LD}=\frac{LI \cos\frac{B}{2}}{LD}=\frac{LI}{LD}\cos\frac{B}{2}=\frac{\sin\frac{A}{2}}{2\cos\frac{C}{2}}=\frac{FJ}{FB}    \]
    结合$\angle DLE=\angle DBE=\frac{B}{2}=\angle BFJ$,故$\triangle DLE \sim \triangle BFJ$
    有$\angle FBJ=\angle LDE=\angle LBE$,即$\angle ABJ=\angle LBI$

如图,在锐角$\triangle ABC$中,$AB>AC$,$M$是$\triangle ABC$的外接圆$\Omega$的劣弧$BC$的中点,$K$是$\angle BAC$的外角平分线与$BC$延长线的交点.在过点$A$且垂直于$BC$的直线上取一点$D$(异于$A$),使得$DM=AM$.设$\triangle ADK$的外接圆与圆$\Omega$相交于点$A$及另一点$T$.证明:$AT$平分线段$BC$

显然$T$的位置不太清楚,但$AT$是根轴是明确的,所以可以直接取出$BC$中点$F$,证明$F$在根轴上.也就是证明$F$对两个圆的幂是相等的.

等等,这不就是今年A1的套路吗?这A2真就和A1这么像都不改的?

$F$对$\bigodot ABC$的幂是$\ds \frac{a^2}{4}$,设$\bigodot ADK$交$BC$于不同于$K$的$E$,只需证明$\ds FE \cdot FK=\frac{a^2}{4}$

考虑外角平分线基本性质$\ds \frac{KB}{KC}=\frac{c}{b}$,可得$\ds KC=\frac{ab}{c-b}$,$\ds KF=\frac{a}{2}+KC=\frac{a(c+b)}{2(c-b)}$
从而只需证明$\ds FE=\frac{a^2}{4}/\frac{a(c+b)}{2(c-b)}=\frac{a(c-b)}{2(c+b)}$
只需证明$\ds CE=FE+\frac{a}{2}=\frac{ac}{c+b}$

可这就是角平分线分割$BC$的两段长度之一,设$AM$交$BC$于$G$,只需证明$BG=CE$,只需证明$MG=ME$,考虑这边还有一个等腰三角形$MA=MD$,只需证明$E,M,D$共线即可
稍微导下角发现就没了

设$\triangle ABC$三边为$a,b,c$,$\bigodot ADK$交$BC$于不同于$K$的$E$,$BC$中点$F$,$AM$交$BC$于$G$.
则有$MF \perp BC$.
考虑$\angle EDA=\angle EKA$(共圆),$\angle EKA=90^\circ-\angle AGK=\angle GAD=\angle MDA$
可得$\angle EDA=\angle MDA$,所以$EMD$三点共线
可得$\angle MEG=\angle MGE=90^\circ-\angle MAD,ME=MG$
由对称性,$\ds CE=BG=\frac{ac}{c+b},FE=CE-\frac{a}{2}=\frac{a(c-b)}{2(c+b)}$
又由外角平分线基本性质$\ds \frac{KB}{KC}=\frac{c}{b}$,可得$\ds KC=\frac{ab}{c-b}$,$\ds FK=\frac{a}{2}+KC=\frac{a(c+b)}{2(c-b)}$
从而$\ds FK \cdot FE=\frac{a(c+b)}{2(c-b)}\frac{a(c-b)}{2(c+b)}=\frac{a^2}{4}=FB \cdot FC$
故$F$在$\bigodot ABC$和$\bigodot ADK$根轴上,即$F$在$AT$上,证毕.