证明:若实数 $a$ 、 $b$ 、 $c$ 满足 $6(b c+c a+a b) \geq 5\left(a^2+b^2+c^2\right)$ ，则对实数 $x$ 、 $y$ 、 $z$ ，有\[    a^2(x-y)(x-z)+b^2(y-z)(y-x)+c^2(z-x)(z- y) \geq 0\]

    考虑\[        6ab \ge 5(a^2+b^2+c^2)-6ac-6bc=5(a-\frac{3}{5}c)^2+5(b-\frac{3}{5}c)^2+\frac{7}{5}c^2 \ge 0    \]
    若$a=0$,显然可得$b=c=0$,下面仅考虑$abc \ne 0$的情况
    此时$a,b,c$任意两个均同号
    不妨设$a,b,c$均为正实数,否则全部反号不影响题目.则有    \begin{gather}        6(a+b)c+\frac{3}{2}(a+b)^2 \ge 6(bc+ca+ab)        \ge 5(a^2+b^2+c^2) \ge 5\times \frac{(a+b)^2}{2}+5c^2\\        (a+b)^2-6(a+b)c+5c^2 \le 0\\        c \le a+b \le 5c    \end{gather}        考虑到将$x,y,z$同时加上一个数原式不变,不妨设$z=0$,则原式化为    \[        a^2 x^2+(c^2-a^2-b^2)xy+b^2 y^2 \ge 0        \]
    只需证    \[        \Delta=(c^2-a^2-b^2)^2-4a^2 b^2=-(a+b+c)(a+b-c)(b+c-a)(c+a-b) \le 0    \]
    而这是显然的,所以原不等式成立.

设 $H, O$ 分别为非等边锐角三角形 $A B C$ 的垂心和外心, 设 $C$ 关于直线 $A B$ 的对称点为 $C^{\prime}, B C^{\prime} \cap A O=L$, 过 $B$ 作关于 $A O$ 的平行线交直线 $A C$ 于点 $Z$, 求证: $\angle L Z B=\angle C Z H$.

解析:容易得$\angle ZBL=90^\circ+A$,结合$\angle HCA=90^\circ-A$,所以我们可以尝试强行构造相似三角形,用SAS的方式证明相似从而得等角.具体如下
    以$H$为圆心,$HC$为半径作圆,交$ZC$于不同于$C$的点$D$,则$\angle ZDH=\angle ZBL=90^\circ+A$
    我们只需证明$\frac{DZ}{DH}=\frac{BZ}{BL}$即可证明原题
    \begin{align}        \frac{BZ}{BL}&=\frac{BZ}{BA}\frac{BA}{BL}\\        &=\frac{\sin A}{\cos B}\frac{\cos A}{\cos C}    \end{align}
    另一方面,考虑$CD=2CH \cdot \cos\angle ACH=2CH\sin A$,以及    \begin{align}        \frac{CZ}{CH}&=\frac{CA+AZ}{AB}\frac{AB}{CH}\\        &=(\frac{CA}{AB}+\frac{AZ}{AB})\frac{AB}{CH}\\        &=(\frac{\sin B}{\sin C}+\frac{\cos C}{\cos B})\frac{\sin C}{\cos C}\\        &=\frac{\sin 2B+\sin 2C}{2\cos B \cos C}\\        &=\frac{\sin(B+C)\cos(B-C)}{\cos B \cos C}\\        &=\sin A \frac{\cos(B-C)}{\cos B \cos C}    \end{align}
    所以    \begin{align}        \frac{DZ}{DH}&=\frac{CZ-2CH\sin A}{DH}=\frac{CZ}{CH}-2\sin A\\        &=\sin A \frac{\cos(B-C)}{\cos B \cos C}-2\sin A\\        &=\sin A \frac{\cos(B-C)-2\cos B \cos C}{\cos B \cos C}\\        &=\sin A \frac{-\cos(B+C)}{\cos B \cos C}\\        &=\frac{\sin A \cos A}{\cos B \cos C}=\frac{BZ}{BL}    \end{align}
    证毕.

设整数 $n \geq 3, a_1, a_2, \cdots, a_n$ 是正实数. 对 $1 \leq i \leq n$, 记 $b_i=\frac{a_{i-1}+a_{i+1}}{a_i}$, 其中 $a_0=a_n, a_{n+1}=a_1$. 已知对任意 $1 \leq i, j \leq n, a_i \leq a_j$ 当且仅当 $b_i \leq b_j$. 求 证: $a_1=a_2=\cdots=a_n$.

 读完题以后应该会有基本的感觉:这两个条件似乎是反的.
    一方面,$a_i$越大,意味着$b_i$越大;另外一方面,$a_i$越大会导致 $b_i=\frac{a_{i-1}+a_{i+1}}{a_i}$要比较小.这两个条件是有矛盾性在里面的.
    那么我们可以考虑$\{a_n\}$的最小项和最大项,设为$a_s,a_t$,则总有    \[        a_s \le a_i \le a_t,\forall 1 \le i \le n    \]
    按照题意我们有$b_s \le b_i \le b_t$,这表明$b_s,b_t$也分别是$b_i$的最小项和最大项
    但是另外一方面,考虑$a_s$最小,$a_t$最大,显然    \[        2 \le \frac{a_{s-1}+a_{s+1}}{a_s} =b_s \le b_t=\frac{a_{t-1}+a_{t+1}}{a_t} \le 2    \]
因此恒有$b_i=2$
既然对一切$1 \le i,j \le n$都有$b_i \le b_j,b_j \le b_i$,那么根据题意,可得$a_i \le a_j,a_j \le a_i$
因此一切$a_i$相同
或者回到递推化成等差数列也行.

对于每个正整数 $k, a_k$ 是最 大的且不能被 3 整除的 $k$ 的约数. 定义数列 $\left\{S_n\right\}$ 为 $S_n=a_1+a_2+\cdots+a_n$ (例如, $S_6=1+2+$ $1+4+5+2)$. 证明: $S_n$ 被 3 整除当且仅当 $n$ 的三进制表示中, 1 的个数可以被 3 整除.

    参考答案的做法比较复杂,我们这里用递推的方式书写.
    首先,如果做本题之前做过另外一个小题,对本题会有所帮助:
    设$a_n$是$n$的最大奇因子,求$S_{2^n}$.
    核心想法是考虑到$a_{2n}=a_n,a_{2n-1}=2n-1$,故    \begin{gather}        S_{2^n}=a_1+a_2+\dots+a_{2^n}\\        =(a_1+a_3+\dots+a_{2^n-1})+(a_2+a_4+\dots+a_{2^n})\\        =(1+3+\dots+(2^n-1))+(a_1+a_2+\dots+a_{2^{n-1}})\\        =(1+3+\dots+(2^n-1))+S_{2^{n-1}}    \end{gather}    再由这个递推式求出$S_{2^n}$
    本题的定义和上题非常类似,我们可以得到    \[        a_{3m+1}=3m+1,a_{3m+2}=3m+2,a_{3m}=a_m,\forall m \in \mn        \]
    于是    \begin{align}        S_{3m}&=a_1+a_2+\dots+a_{3m}\\        &=1+2+4+5+\dots+(3m-2)+(3m-1)+(a_3+a_6+a_9+\dots+a_{3m})\\        &=3+9+\dots+(6m-3)+S_m \\        &\equiv S_m \pmod 3    \end{align}
    这样就得到了$S_{3m}$和$S_m$的关系式.而题目中描述的三进制表达式也就自然而然出现了:    \[        S_{3m+1}\equiv 3m+1+S_{3m} \equiv S_m+1 \pmod 3    \]    \[        S_{3m+2}\equiv (3m+1)+(3m+2)+S_{3m} \equiv S_m \pmod 3    \]
    概括而言,就是引理:        \[        S_{3m+b} \equiv \delta(b)+S_m \pmod 3,b=0,1,2    \]    其中$\delta(1)=1,\delta(0)=\delta(2)=0$
    设$n$的三进制表达为$\sum_{j=0}^k b_j \cdot 3^j,b_j \in \{0,1,2\},\forall j =0,1,2,\dots,k$,且$b_k \ne 0$
    那么我们就有    \[        n=b_0+3(b_1+b_2 \cdot 3+\dots+b_k \cdot 3^{k-1})    \]

    对$k$归纳:    \[        S(\sum_{j=0}^k b_j \cdot 3^j) \equiv \sum_{j=0}^k \delta(b_j) \pmod 3        \]    当$k=0$容易验证成立

    假设对$k-1$成立,则$S(b_1+b_2 \cdot 3+\dots+b_k \cdot 3^{k-1}) \equiv \sum_{j=1}^k \delta(b_j) \pmod 3$
    考虑    \[        \sum_{j=0}^k b_j \cdot 3^j=b_0+3(b_1+b_2 \cdot 3+\dots+b_k \cdot 3^{k-1})    \]
    使用上面的引理可得
    \begin{align}        S(\sum_{j=0}^k b_j \cdot 3^j) &\equiv \delta(b_0)+S(b_1+b_2 \cdot 3+\dots+b_k \cdot 3^{k-1}) \\        &\equiv \delta(b_0)+\sum_{j=1}^k \delta(b_j) \\        &\equiv \sum_{j=0}^k \delta(b_j) \pmod 3    \end{align}
    则对$k+1$也成立

 设 $\left\{a_n\right\} 、\left\{b_n\right\}(n=1,2, \cdots)$ 是两个整数数列, $a_1=1, b_1=0$, 且对于 $n \geqslant 1$, $a_{n+1}=7 a_n+12 b_n+6, b_{n+1}=4 a_n+7 b_n+3$.证明: $a_n^2$ 是两个连续立方数的差.

待定$\lambda$使得$a_n+\lambda b_n$能构成一个类等比数列    \[        a_{n+1}+\lambda b_{n+1}=(7+4\lambda)a_n+(12+7\lambda)b_n+6+3\lambda        \]        满足$12+7\lambda=\lambda (7+4\lambda),\lambda^2=3$
    \[        a_{n+1}+\lambda b_{n+1}=(7+4\lambda)(a_n+\lambda b_n)+6+3\lambda=(7+4\lambda)(a_n+\lambda b_n)+2\lambda^2+3\lambda    \]
    于是    \[        a_{n+1}+\lambda b_{n+1}+\frac{\lambda}{2}=(7+4\lambda)(a_n+\lambda b_n+\frac{\lambda}{2})        \]        代入$\lambda=\pm \sqrt{3}$,并且两式相加可得    \[        2a_n=\frac{(2+\sqrt{3})^{2n-1}+(2-\sqrt{3})^{2n-1}}{2}        \]        设$a_n^2=(x+1)^3-x^3=3x^2+3x+1$,则当$n$充分大时,$a_n \sim \sqrt{3} x$
    于是$x \sim \frac{2a_n}{2\sqrt{3}}$,我们可以断言$x$大约等于$\frac{(2+\sqrt{3})^{2n-1}}{4\sqrt{3}}$
    补上共轭式使它有理化,变成    \[        \frac{(2+\sqrt{3})^{2n-1}-(2-\sqrt{3})^{2n-1}}{4\sqrt{3}}    \]
    代入1发现还差$\frac{1}{2}$,于是最终得到    \[        x_n=\frac{(2+\sqrt{3})^{2n-1}-(2-\sqrt{3})^{2n-1}}{4\sqrt{3}}+\frac{1}{2}    \]
    接下来只需证明两件事:$a_n^2=3x_n^2+3x_n+1$,以及$x_n \in \mn$
    前者只需要代入通项,后者只需要回到二阶线性递推.

    当然,你有本事看出来$x_n=b_n+1$也行

前段时间网站被黑,服务器没有来得及维护,东西丢了不少,服务器停了很久.而今找回,重新布置上线.

 

已知 $a \geq b \geq c \geq d \geq 0$, 且 $\ds \frac{a^2+b^2+c^2+d^2}{(a+b+c+d)^2}=\frac{3}{8}$, 求 $\ds \frac{a+c}{b+d}$ 的最大值

考虑    \begin{align}        \frac{3}{8}(a+b+c+d)^2&=a^2+b^2+c^2+d^2\\        & \ge a^2+c^2+c^2+0=a^2+2c^2\\        & \ge \frac{(a+c)^2}{1+\frac{1}{2}}\\        \frac{9}{16}(a+b+c+d)^2 &\ge (a+c)^2\\        \frac{a+c}{b+d} & \le 3    \end{align}    当$a=2,b=c=1,d=0$可取等

12. 设不全相等的三个复数 $z_1, z_2, z_3$ 满足方程 $4 z_1^2+5 z_2^2+5 z_3^2=4 z_1 z_2+6 z_2 z_3+4 z_3 z_1$. 记复平面 上以 $z_1, z_2, z_3$ 为顶点的三角形三边的长从小到大依次为 $a, b, c$, 则 $a: b: c=\tk$

解:作为填空本题非常简单,只需令$z_3=0$,立即可得\[    4z_1^2+5z_2^2-4z_1 z_2=0    \]
显然\[    (2z_1-z_2)^2+z_2^2=0,2z_1-z_2=\pm 2\mi z_2    \]
取$z_1=1\pm 2\mi,z_2=2$,结合$z_3=0$,可得三边依次为$2,\sqrt{5},\sqrt{5}$
如果采用严格的证明方式做也不复杂.
由于要求的是边之间的关系,这就意味着中间会反复出现$z_1-z_2,z_2-z_3,z_3-z_1$这种东西
稍微观察会发现原式可以化为\[    2(z_1-z_2)^2+3(z_2-z_3)^2+2(z_3-z_1)^2=0    \]
使用$z_1$作为起点整理\[    2(z_2-z_1)^2+3[(z_2-z_1)-(z_3-z_1)]^2+2(z_3-z_1)^2=0    \]
即\[    5(z_2-z_1)^2-6(z_2-z_1)(z_3-z_1)+5(z_3-z_1)^2=0    \]
也就是说$\frac{z_3-z_1}{z_2-z_1}$是方程$5x^2-6x+5=0$的根\[    x=\frac{6 \pm 8\mi}{10}=\frac{3 \pm 4\mi}{5}    \]
取$z_3-z_1=3 \pm 4\mi,z_2-z_1=5$,则$z_3-z_2=-2\pm 4\mi$
可得三边之比为$2:\sqrt{5}:\sqrt{5}$

本题为本次预赛压轴填空,主要考察的是复数的几何意义.

已知$x+y=3$,求下式的最大值\[    \frac{x^2+y^2+2}{\sqrt{(x^2+1)(y^2+1)}}    \]

解:\begin{align}    13(x^2+1)(y^2+1)&=(9+4)[(x+y)^2+(1-xy)^2]\\    &\ge [3(x+y)+2(1-xy)]^2=[(x+y)^2+2(1-xy)]^2\\    &=(x^2+y^2+2)^2\end{align}
故可得\[    \frac{x^2+y^2+2}{\sqrt{(x^2+1)(y^2+1)}} \le \sqrt{13}    \]
当$xy=-1$取等,解方程可得具体取等条件

2023中国TST测试3第4题

4. 如图, 圆 $\Gamma, \Gamma_1, \Gamma_2$ 两两外切, 且均与直线 $l$ 相切. 设 $\Gamma, \Gamma_1$ 切于点 $B_1, \Gamma, \Gamma_2$ 切于 点 $B_2, \Gamma_1, \Gamma_2$ 切于点$C$. $\Gamma, \Gamma_1, \Gamma_2$ 分别与 $l$ 切于点 $A, A_1, A_2$, 其中 $A$ 在线段 $A_1 A_2$ 上. 设直 线 $A_1 C, A_2 B_2$ 交于点 $D_1$, 直线 $A_2 C, A_1 B_1$ 交于点 $D_2$. 求证: $D_1 D_2 / / l$.

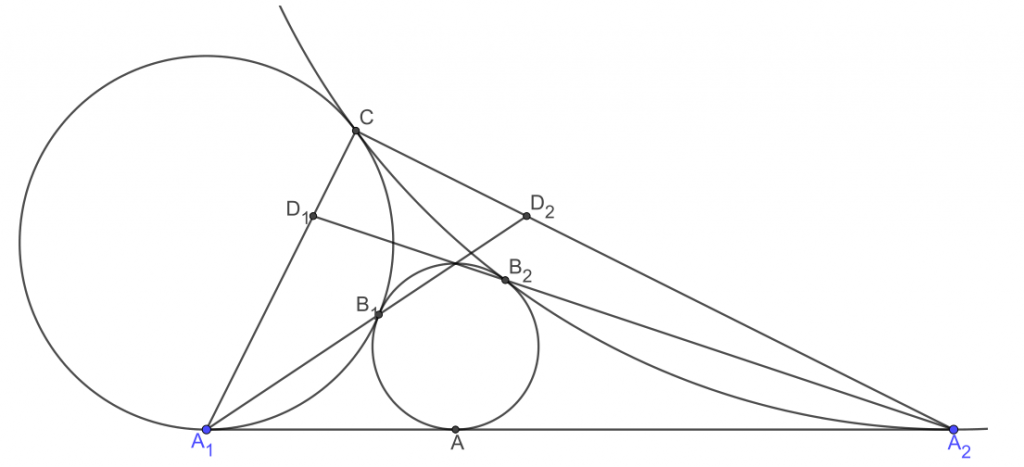
解析:本题初看圆很多很复杂,但是略加分析会发现其中大部分长度都是可表示的.这会提示我们用计算法.(实际上如果给定$\Gamma$的话,$\Gamma_1,\Gamma_2$的圆心在同一个定抛物线上).

    设$\Gamma,\Gamma_1,\Gamma_2$的圆心分别为$O,O_1,O_2$,半径分别为$1,r,R$.$AA_1=2x,AA_2=2y$,不妨设$x<y$
    则对$O_1 O A A_1$使用勾股定理(省略垂线那一步)可得    \[        (r+1)^2=(r-1)^2+(2x)^2,r=x^2        \]        同理$R=y^2$
    再对$O_1 O_2 A_2 A_1$使用勾股定理    \[        (R+r)^2=(R-r)^2+(2x+2y)^2        \]        解得    \[        4(x+y)^2=4Rr=4x^2 y^2,x+y=xy        \]        到这里为止,我们找到了三个圆的全部限制.由于表达式非常友好(整式多项式),就算暴力手段也是可以接受的.但是我们仍然想要尽可能的简化计算.

一开始我考虑计算($[XYZ]$表示$\triangle XYZ$的面积)    \[        \frac{[A_1 B_1 C]}{[A_1 B_1 A_2]}=\frac{[A_2 B_2 C]}{[A_2 B_2 A_1]}        \]        这样可以得到$\frac{CD_2}{D_2 A_2}=\frac{CD_1}{D_1 A_1}$,就完成了证明.但是尝试之后发现计算还是复杂了些.

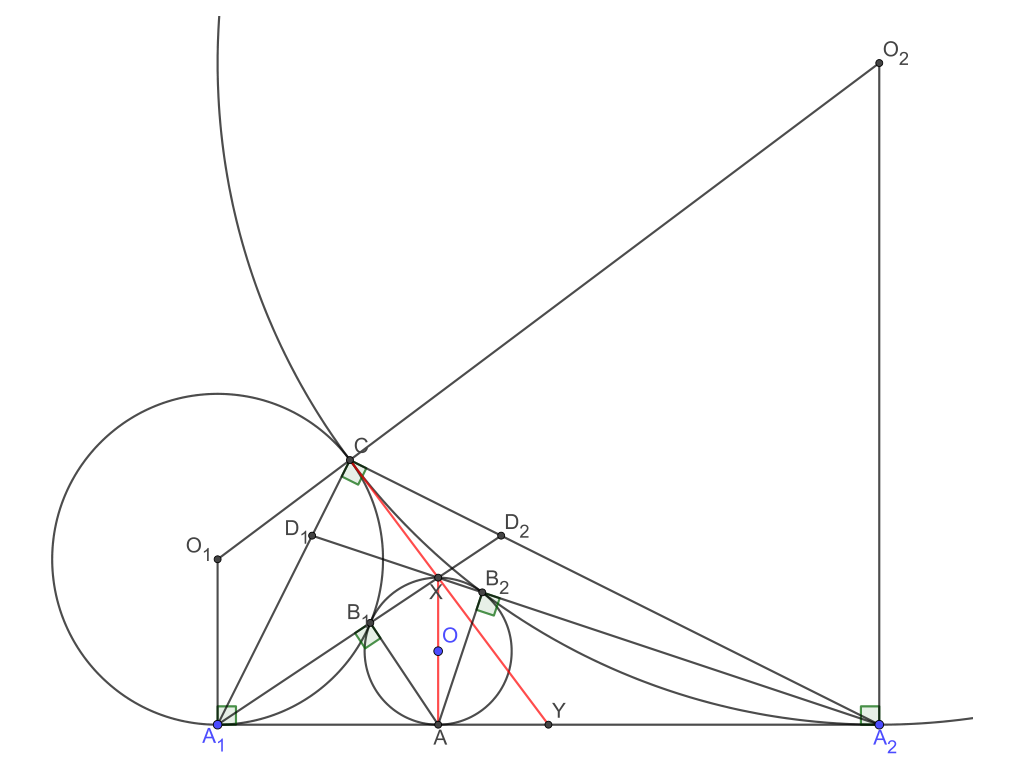
最终转而证明$A_1 B_1 \cap A_2 B_2$在$C$和$A_1 A_2$中点的连线上.这样配合塞瓦就能证明$D_1 D_2 // l$了
    设$A_1 B_1 \cap A_2 B_2=X$,$A_1 A_2$中点为$Y$.
    基本性质:$\angle A_1 B_1 A=\angle A_2 B_2 A=\angle A_1 C A_2=90^\circ$(作公切线,或者导弦切角) 
    所以$A B_1 X B_2$共圆,也就是说$AX$是$\Gamma$的直径.$AX \perp l,AX=2$
由$AY=y-x$可得,    \[        \tan AYX=\frac{AX}{AY}=\frac{2}{y-x}        \]        由于$CY$是$\Gamma_1,\Gamma_2$公切线,所以$\angle AYC=\angle A_2 O_2 C=2\angle A_2 O_2 Y$
考虑到$xy=x+y$    \[        \tan \angle A_2 O_2 Y=\frac{A_2 Y}{A_2 O_2}=\frac{x+y}{y^2}=\frac{x}{y}        \]
进而    \[        \tan AYC=\tan 2\angle A_2 O_2 Y=\frac{2 \cdot \frac{x}{y}}{1-\left(\frac{x}{y}\right)^2}=\frac{2xy}{(y-x)(y+x)}=\frac{2}{y-x}        \]
这表明$\angle AYC=\angle AYX$,$C,X,Y$三点共线
由塞瓦定理    \[        \frac{CD_2}{D_2 A_2}\frac{A_2 Y}{YA_1}\frac{A_1 D_1}{D_1 C}=1        \]
    \[        \frac{CD_2}{D_2 A_2}=\frac{C D_1}{D_1 A}        \]        所以$D_1 D_2 //l$

    最终我们并没有采用纯粹的计算法,用的是计算和几何性质结合的方式.就难度来说,大概在联赛第2题?从联赛到冬令营到集训队测试,好像没感觉几何题难度有太多上升….

学校发的小题专练里的题目
12. 已知函数 $f(x)=2 \sin (\omega x+\varphi)+h$ 的最小正周期为 $\pi$, 若 $|f(x)|$ 在 $\left[0, \frac{\pi}{4}\right]$ 上的最大值为 $M$, 则 $M$ 的最小值为$\tk$

解:考虑$f(0)=2\sin\varphi +h,f(\frac{\pi}{8})=\sqrt{2}\sin\varphi+\sqrt{2}\cos\varphi+h,f(\frac{\pi}{4})=2\cos\varphi+h$
\begin{gather}    2M \ge |f(0)-f(\frac{\pi}{8})|=|(2-\sqrt{2})\sin\varphi-\sqrt{2}\cos\varphi|\\    2M \ge |f(\frac{\pi}{4})-f(\frac{\pi}{8})|=|(2-\sqrt{2})\cos\varphi-\sqrt{2}\sin\varphi|\\    (2M)^2+(2M)^2 \ge |(2-\sqrt{2})\sin\varphi-\sqrt{2}\cos\varphi|^2+|(2-\sqrt{2})\cos\varphi-\sqrt{2}\sin\varphi|^2\\    =8-4\sqrt{2}-(4\sqrt{2}-4)\sin 2\varphi \ge 12-8\sqrt{2}\\    M \ge \frac{2-\sqrt{2}}{2}\end{gather}当$\varphi=\frac{3\pi}{4},h=-\frac{2+\sqrt{2}}{2}$取等