2023中国TST测试3第4题

4. 如图, 圆 $\Gamma, \Gamma_1, \Gamma_2$ 两两外切, 且均与直线 $l$ 相切. 设 $\Gamma, \Gamma_1$ 切于点 $B_1, \Gamma, \Gamma_2$ 切于 点 $B_2, \Gamma_1, \Gamma_2$ 切于点$C$. $\Gamma, \Gamma_1, \Gamma_2$ 分别与 $l$ 切于点 $A, A_1, A_2$, 其中 $A$ 在线段 $A_1 A_2$ 上. 设直 线 $A_1 C, A_2 B_2$ 交于点 $D_1$, 直线 $A_2 C, A_1 B_1$ 交于点 $D_2$. 求证: $D_1 D_2 / / l$.

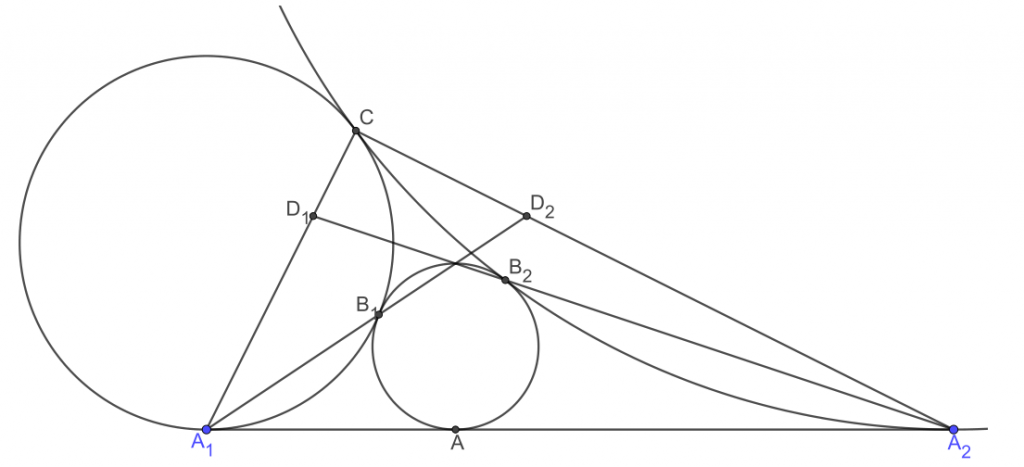
解析:本题初看圆很多很复杂,但是略加分析会发现其中大部分长度都是可表示的.这会提示我们用计算法.(实际上如果给定$\Gamma$的话,$\Gamma_1,\Gamma_2$的圆心在同一个定抛物线上).

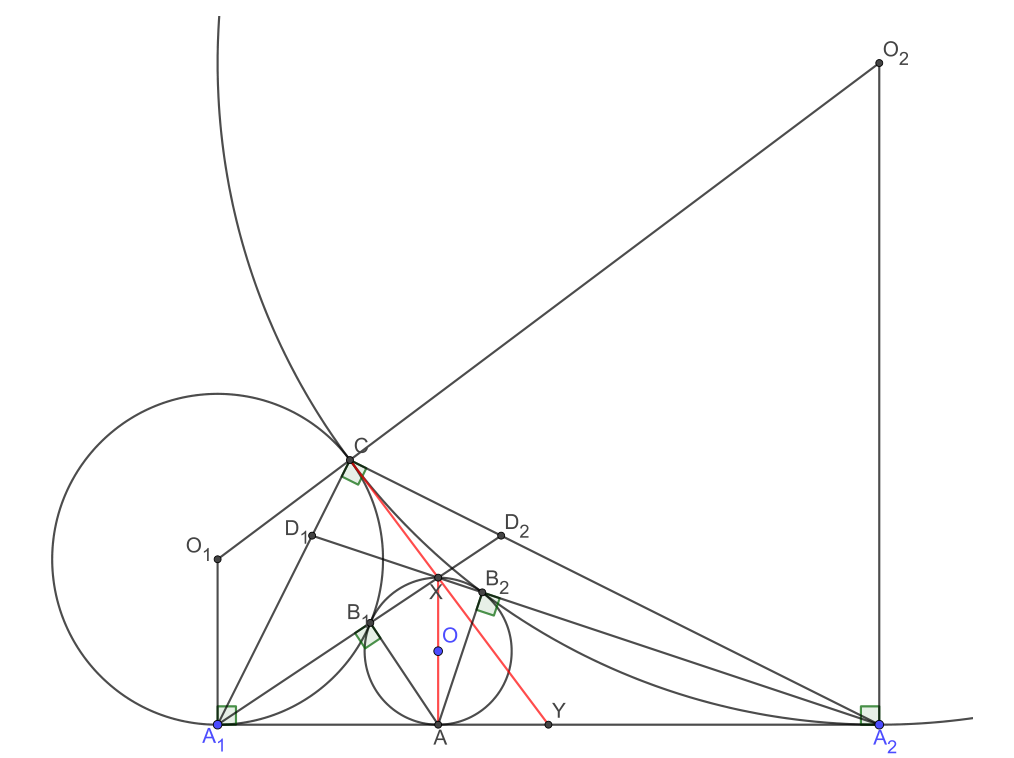
    设$\Gamma,\Gamma_1,\Gamma_2$的圆心分别为$O,O_1,O_2$,半径分别为$1,r,R$.$AA_1=2x,AA_2=2y$,不妨设$x<y$
    则对$O_1 O A A_1$使用勾股定理(省略垂线那一步)可得    \[        (r+1)^2=(r-1)^2+(2x)^2,r=x^2        \]        同理$R=y^2$
    再对$O_1 O_2 A_2 A_1$使用勾股定理    \[        (R+r)^2=(R-r)^2+(2x+2y)^2        \]        解得    \[        4(x+y)^2=4Rr=4x^2 y^2,x+y=xy        \]        到这里为止,我们找到了三个圆的全部限制.由于表达式非常友好(整式多项式),就算暴力手段也是可以接受的.但是我们仍然想要尽可能的简化计算.

一开始我考虑计算($[XYZ]$表示$\triangle XYZ$的面积)    \[        \frac{[A_1 B_1 C]}{[A_1 B_1 A_2]}=\frac{[A_2 B_2 C]}{[A_2 B_2 A_1]}        \]        这样可以得到$\frac{CD_2}{D_2 A_2}=\frac{CD_1}{D_1 A_1}$,就完成了证明.但是尝试之后发现计算还是复杂了些.

最终转而证明$A_1 B_1 \cap A_2 B_2$在$C$和$A_1 A_2$中点的连线上.这样配合塞瓦就能证明$D_1 D_2 // l$了
    设$A_1 B_1 \cap A_2 B_2=X$,$A_1 A_2$中点为$Y$.
    基本性质:$\angle A_1 B_1 A=\angle A_2 B_2 A=\angle A_1 C A_2=90^\circ$(作公切线,或者导弦切角) 
    所以$A B_1 X B_2$共圆,也就是说$AX$是$\Gamma$的直径.$AX \perp l,AX=2$
由$AY=y-x$可得,    \[        \tan AYX=\frac{AX}{AY}=\frac{2}{y-x}        \]        由于$CY$是$\Gamma_1,\Gamma_2$公切线,所以$\angle AYC=\angle A_2 O_2 C=2\angle A_2 O_2 Y$
考虑到$xy=x+y$    \[        \tan \angle A_2 O_2 Y=\frac{A_2 Y}{A_2 O_2}=\frac{x+y}{y^2}=\frac{x}{y}        \]
进而    \[        \tan AYC=\tan 2\angle A_2 O_2 Y=\frac{2 \cdot \frac{x}{y}}{1-\left(\frac{x}{y}\right)^2}=\frac{2xy}{(y-x)(y+x)}=\frac{2}{y-x}        \]
这表明$\angle AYC=\angle AYX$,$C,X,Y$三点共线
由塞瓦定理    \[        \frac{CD_2}{D_2 A_2}\frac{A_2 Y}{YA_1}\frac{A_1 D_1}{D_1 C}=1        \]
    \[        \frac{CD_2}{D_2 A_2}=\frac{C D_1}{D_1 A}        \]        所以$D_1 D_2 //l$

    最终我们并没有采用纯粹的计算法,用的是计算和几何性质结合的方式.就难度来说,大概在联赛第2题?从联赛到冬令营到集训队测试,好像没感觉几何题难度有太多上升….

11. 已知 $F$ 是双曲线 $E: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左焦点, $P$ 是 $E$ 右支上一点, $P F$ 与 $E$ 的渐近 线分别交于 $A, B$ 两点, 且 $\overrightarrow{F A}=\overrightarrow{A B}=2 \overrightarrow{B P}$, 则 $E$ 的离心率为$\tk$

解:我们令$X$代指$A$或者$B$,设$\vv{FX}=\lambda \vv{FP}$,由题意可知$\lambda=\frac{2}{5},\frac{4}{5}$(分别对应$A$和$B$)
            设$P(x_1,y_1),\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}=1$,则有            \[                X(\lambda x_1+c(\lambda-1),\lambda y_1)                \]                        代入渐近线方程            \[                \frac{x^2}{a^2}-\frac{y^2}{b^2}=0                \]                        可得            \begin{gather}                \frac{[\lambda x_1+c(\lambda-1)]^2}{a^2}-\frac{(\lambda y_1)^2}{b^2}=0\\                 \lambda^2+\frac{2cx_1\lambda(\lambda-1)}{a^2}+\frac{c^2(\lambda-1)^2}{a^2}=0\\                c^2(\frac{\lambda-1}{\lambda})^2+2cx_1 \frac{\lambda-1}{\lambda}+a^2=0            \end{gather}            注意到$\frac{\lambda-1}{\lambda}=-\frac{3}{2},-\frac{1}{4}$,由韦达定理            \[                \frac{a^2}{c^2}=(-\frac{3}{2}) \cdot (-\frac{1}{4})=\frac{8}{3}                \]                        \[                \frac{c}{a}=\sqrt{\frac{8}{3}}=\frac{2\sqrt{6}}{3}                \] 

12. 若 $a=\mathrm{e}^{0.2} \ln 3, b=\mathrm{e}^{0.3} \ln 2, c=\frac{\mathrm{e}^{0.4}}{3}$, 则请比较大小 

解:基本常识:$\ln 2$大约是0.7                               
$\me^{0.1}$只比1.1大一点.如果非要证明的话,$f(x)=\me^x-1-2x$的导数$f'(x)=\me^x-2<0,\forall 0<x<\frac{1}{2}$,故$\me^x<1+2x,\forall 0<x<\frac{1}{2}$.因此$\me^{0.1}<1.2$
                \[                    \frac{c}{b}=\frac{\me^{0.1}}{3\ln 2} \approx \frac{\me^{0.1}}{2.1}<1                    \]
                基本常识:$3>2\sqrt{2},\ln 3>\frac{3}{2}\ln2$                \[                    \frac{b}{a}=\frac{\me^{0.1}\ln 2}{\ln 3}<\frac{2}{3}\me^{0.1}<1                    \]
                因此$c<b<a$

20. (12 分)已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的长轴长为 $4, O$ 为坐标原点, $A$ 为椭圆 $C$ 的右顶点, $B$ 为 椭圆 $C$ 的上顶点,且 $\triangle A B O$ 的面积为 $\sqrt{3}$.                         
(1)求椭圆 $C$ 的方程.                               
(2) 过点 $D(2,3)$ 的直线 $l$ 与椭圆相交于 $P, Q$ 两点, 过点 $P$ 作 $x$ 轴的垂线, 与直线 $A Q$ 相交 于点 $M, N$ 是 $P M$ 的中点, 试问直线 $A N$ 的斜率是否为定值? 若是, 求出该定值; 若不 是, 说明理由.         

解:本题使用常规方法直接算即可,属于对称型问题,不需太多技巧.而实质上本题还是与22年乙卷题目相通的题目.由于$N$是$PM$中点,故$AM,AP;AN,AD$是调和线束,而$AD$是椭圆切线,所以$AN$就是$D$对应的切点弦所在直线.切线产生的调和,中线产生的调和,本题具有与22年乙卷完全相同的命题背景,但是简单在不需要猜点,计算也是完全对称化的.
当然,这里仍然可以采用点生成点的方式:
                $P(x,_1,y_1),Q(x_2,y_2)$,设$\vv{DQ}=\lambda \vv{DP},x_2=\lambda x_1+2(1-\lambda),y_2=\lambda y_1+3(1-\lambda)$
                代入到$\frac{x_2^2}{4}+\frac{y_2^2}{3}=1$,可得                \[                    \lambda=\frac{3}{5-x_1-2y_1}                    \]
                从而$M$的纵坐标                \[                    y_M=\frac{y_2}{x_2-2}(x_1-2)=\frac{\lambda(y_1-3)+3}{\lambda}=2-x_1-y_1                    \]                                从而                \[                    N(x_1,\frac{2-x_1}{2})                    \]
                所以$AN$的斜率为                \[                    \frac{\frac{2-x_1}{2}-0}{x_1-2}=-\frac{1}{2}                    \]

21. (12 分)已知 $a \in \mathbf{R}$, 函数 $f(x)=\frac{2}{\sqrt{x}}+a x$.
(1)讨论 $f(x)$ 的单调性;
(2) 设 $[x]$ 表示不超过 $x$ 的最大整数, 证明: $\left[\sqrt{\frac{1^2+1}{1^2+1+1}}+\sqrt{\frac{2^2+2}{2^2+2+1}}+\cdots+\sqrt{\frac{n^2+n}{n^2+n+1}}\right]$ $=n-1, n \in \mathbf{N}^{\cdot}$.

证明:记$S_n=\sqrt{\frac{1^2+1}{1^2+1+1}}+\sqrt{\frac{2^2+2}{2^2+2+1}}+\cdots+\sqrt{\frac{n^2+n}{n^2+n+1}}$
    注意到    \[        0<1-\sqrt{\frac{n^2+n}{n^2+n+1}}=\frac{\frac{1}{n^2+n+1}}{1+\sqrt{\frac{n^2+n}{n^2+n+1}}}<\frac{1}{n^2+n+1}<\frac{1}{n}-\frac{1}{n+1}        \]
    可得    \[        0<n-S_n<1-\frac{1}{n+1},n-1+\frac{1}{n+1}<S_n<n        \]        故$[S_n]=n-1$

学校发的小题专练里的题目
12. 已知函数 $f(x)=2 \sin (\omega x+\varphi)+h$ 的最小正周期为 $\pi$, 若 $|f(x)|$ 在 $\left[0, \frac{\pi}{4}\right]$ 上的最大值为 $M$, 则 $M$ 的最小值为$\tk$

解:考虑$f(0)=2\sin\varphi +h,f(\frac{\pi}{8})=\sqrt{2}\sin\varphi+\sqrt{2}\cos\varphi+h,f(\frac{\pi}{4})=2\cos\varphi+h$
\begin{gather}    2M \ge |f(0)-f(\frac{\pi}{8})|=|(2-\sqrt{2})\sin\varphi-\sqrt{2}\cos\varphi|\\    2M \ge |f(\frac{\pi}{4})-f(\frac{\pi}{8})|=|(2-\sqrt{2})\cos\varphi-\sqrt{2}\sin\varphi|\\    (2M)^2+(2M)^2 \ge |(2-\sqrt{2})\sin\varphi-\sqrt{2}\cos\varphi|^2+|(2-\sqrt{2})\cos\varphi-\sqrt{2}\sin\varphi|^2\\    =8-4\sqrt{2}-(4\sqrt{2}-4)\sin 2\varphi \ge 12-8\sqrt{2}\\    M \ge \frac{2-\sqrt{2}}{2}\end{gather}当$\varphi=\frac{3\pi}{4},h=-\frac{2+\sqrt{2}}{2}$取等

设$a \ge 0$,函数$f(x)=(x+1)\ln x+(a-2)x+2$
求证:(1)$f(x)$存在唯一零点$x_0$;
(2)若$x_1+a=\sin x_1$,则$x_1-\ln x_0 \le 0$

证明:第一问可以证$f(x)$单调递增,略
第二问:用$a$表示$x_1$是不现实的,所以我们整体将$f(x)$中的$a$换成$x_1-\sin x_1$
考虑$f(x)$的单调性\[    x_1-\ln x_0 \le 0 \iff \me^{x_1} \le x_0 \iff f(\me^{x_1}) \le f(x_0)=0    \]\[    \iff f(\me^{x_1})=(\me^{x_1}+1)x_1+(\sin x_1-x_1-2)\me^{x_1}+2=(\sin x_1-2)\me^{x_1}+x_1+2 \le 0    \]
    定义函数$g(x)=(\sin x-2)\me^x+x+2,g(x_1)=f(\me^{x_1})$
    则\[        g'(x)=\me^x(\sin x+\cos x-2)+1,g”(x)=2\me^x (\cos x-1) \le 0        \]
可得$g'(x)$在$\mr$上单调递减
所以当$x>0,g'(x)<g'(0)=0$;当$x<0,g'(x)>g'(0)=0$
故$g(x)$在$(-\infty,0)$单调递增,$(0,+\infty)$单调递减
$f(\me^x_1)=g(x_1) \ge g(0)=0$,故结论成立

锐角三角形$ABC$中，$D,E,F$为$BC，AC,AB$中点，$X,Y$为$D$在$AB$,$AC$上垂足，过$F$且与$XY$平行的直线与$DY$交于$P$。求证：$AD \perp EP$。

需要知道面积与定比分点的公式

注意到$AD \perp EP \iff$ $E$是$\triangle APD$垂心
\begin{gather}    AD \perp EP \iff AP \perp DE \iff AP //XD \\    \iff [PDX]=[ADX] \iff [FYX]+[DYX]=[ADX] \\    \iff \frac{1}{2}([XAY]-[XBY])+\frac{1}{2}([BXY]+[CXY])=[ADX]\\    \iff \frac{1}{2}([XAY]+[XCY])=[ADX]\end{gather}考虑到\[    [XAY]+[XCY]=[ACX]=2[ADX]    \]结论显然成立

设正整数数列$\{a_n\}$满足:$a_2=4$,且对任何$n \in \mN$,有    \[        2+\frac{1}{a_{n+1}}<\frac{\frac{1}{a_n}+\frac{1}{a_{n+1}}}{\frac{1}{n}-\frac{1}{n+1}}<2+\frac{1}{a_n}        \]        求$\{a_n\}$的通项公式

不等式定义的正整数数列,那肯定是写几项用归纳法了.

    解:代入$n=1$,得$\ds \frac{2}{3}<a_1<\frac{8}{7},a_1=1$,类似的可以求得$a_3=9$.猜测$a_k=k^2(\forall k \ge 2)$,下面用归纳法证明.

    显然$k=2$时成立,假设对$k$成立,即$a_k=k^2$,代入$n=k$:
    由于\[        2+\frac{1}{a_{k+1}}<(\frac{1}{k^2}+\frac{1}{a_{k+1}})k(k+1)        \]        可得    \[        a_{k+1}<\frac{k(k^2+k-1)}{k-1}=(k+1)^2+\frac{1}{k-1} \le (k+1)^2+1        \]
    考虑$a_{k+1}$是正整数,可得$a_{k+1} \le (k+1)^2$
    另外一方面    \[        (\frac{1}{k^2}+\frac{1}{a_{k+1}})k(k+1)<2+\frac{1}{k^2}        \]
    可得    \[        a_{k+1}>\frac{k(k+1)}{1-\frac{1}{k}+\frac{1}{k^2}}        \]        我们尝试证明    \begin{gather}        \frac{k(k+1)}{1-\frac{1}{k}+\frac{1}{k^2}} \ge k^2+2k\\        \Longleftrightarrow \frac{k+1}{k+2} \ge 1-\frac{1}{k}+\frac{1}{k^2}\\        \Longleftrightarrow \frac{1}{k}-\frac{1}{k^2} \ge \frac{1}{k+2}\\        \Longleftrightarrow \frac{1}{k}-\frac{1}{k+2} \ge \frac{1}{k^2}\\        \Longleftrightarrow \frac{2}{k(k+2) \ge \frac{1}{k^2}}\\        \Longleftrightarrow k \ge 2    \end{gather}    故可得$a_{k+1}>k^2+2k,a_{k+1} \ge k^2+2k+1=(k+1)^2$
    结合$a_{k+1} \le (k+1)^2$,可得$a_{k+1}=(k+1)^2$
    归纳原理可知对一切正整数$n$,$a_n=n^2$\end{proof}

设十进制$n$位正整数中,任何相邻两位数字(从左到右)不出现12的数有$a_n$个.证明:对任意$n \in \mN$,有$\ds \frac{1}{2}(a_n a_{n+1}-1)$是完全平方数

证明:
约定:如果一个正整数的任何相邻两位数字(从左到右)不出现12,则我们称为它具有性质$P$
    显然有$a_1=9,a_2=89,a_3=889$
    考虑$n+1$位具有性质$P$的正整数,有$a_{n+1}$个
    另外一方面,若尾数为2,则它的前$n$位是具有性质$P$且末尾不是1的正整数.具有性质$P$的$n$位正整数有$a_n$个,其中末尾是1的有$a_{n-1}$个,故此时有$a_n-a_{n-1}$个
    若尾数不是2,则尾数有9种可能,前$n$位有$a_n$种可能,此时有$9a_n$个
    因而,$a_{n+1}=(a_n-a_{n-1})+9a_{n}=10a_n-a_{n-1}$    \[        \frac{a_{n+1}+a_{n-1}}{a_n}=10=\frac{a_{n+2}+a_n}{a_{n+1}}        \]    可得    \[        a_{n+1}^2+a_{n+1}a_{n-1}=a_n a_{n+2}+a_n^2,a_{n+1}^2-a_{n+2}a_n=a_n^2-a_{n+1}a_{n-1}        \]    这表明$a_n^2-a_{n+1}a_{n-1}$是常数,为$-8$
    从而    \[        a_{n+1}^2-10a_{n}a_{n+1}+a_n^2=a_{n+1}(a_{n+1}-10a_n)+a_n^2=a_n^2-a_{n+1}a_{n-1}=-8        \]
    故    \[        8a_n a_{n+1}-8=8a_n a_{n+1}+a_{n+1}^2-10a_{n}a_{n+1}+a_n^2=(a_{n+1}-a_n)^2        \]            由于$8 \mid (a_{n+1}-a_n)^2$,故$4 \mid a_{n+1}-a_n$
    故$\ds \frac{1}{2}(a_n a_{n+1}-1)=\left(\frac{a_{n+1}-a_n}{2}\right)^2$是完全平方数

585. 已知数列 $\left\{x_n\right\}$ 满足: $\ds x_1=\frac{1}{2}, x_{n+1}=\frac{1}{1+x_n}, n \in \mathbf{N}^*$, 求证: $\ds \left|x_2-x_1\right|+\left|x_3-x_2\right|+\cdots+\left|x_{n+1}-x_n\right|<\frac{1}{3}$.

证明:归纳证明:$\forall n \in \mN,\frac{1}{2} \le x_n \le \frac{2}{3}$
显然$n=1$成立
设$n$成立,$\frac{1}{2} \le x_n \le \frac{2}{3}$,则由$x_{n+1}=\frac{1}{1+x_n}$\[    \frac{1}{1+\frac{2}{3}} \le x_{n+1} \le \frac{1}{1+\frac{1}{2}}\]即有\[    \frac{1}{2}<\frac{3}{5} \le x_{n+1} \le \frac{2}{3}    \]对$n+1$也成立.故原命题成立.
从而有$(1+x_n)(1+x_{n-1}) \ge \frac{9}{4}$\[    |x_{n+1}-x_n|=|\frac{1}{1+x_n}-\frac{1}{1+x_{n-1}}|=\frac{|x_n-x_{n-1}|}{(1+x_n)(1+x_{n-1})}\\    \le \frac{4}{9}|x_n-x_{n-1}|    \]
结合$|x_2-x_1|=\frac{1}{6}$,可得\[    |x_{n+1}-x_n| \le (\frac{4}{9})^{n-1} \cdot \frac{1}{6}    \]
求和可得\[    \sum_{k=1}^n |x_{k+1}-x_k| \le \sum_{k=1}^n (\frac{4}{9})^{n-1} \cdot \frac{1}{6} < \sum_{k=1}^\infty (\frac{4}{9})^{n-1} \cdot \frac{1}{6} =\frac{3}{10}<\frac{1}{3}    \]

正项数列 $\left\{x_n\right\}$ 满足 $x_n+\frac{1}{x_{n+1}}<2, n \in \mN$
(1) 证明: $x_n<x_{n+1}$
(2) 证明: $1-\frac{1}{n}<x_n<1$

证明:(1) 均值不等式\[    x_{n+1}+\frac{1}{x_{n+1}} \ge 2 > x_n+\frac{1}{x_{n+1}}\]
故有$x_{n+1}>x_n$

(2) 若存在某个$x_k\ge 1$,那么由(1)可得$x_n>1,\forall n>k$
\begin{gather}    \forall n \ge k+1,0<x_n-1<\frac{x_{n+1}-1}{x_{n+1}}\\    \frac{1}{x_n-1}>\frac{x_{n+1}}{x_{n+1}-1}=1+\frac{1}{x_{n+1}-1},\frac{1}{x_{n+1}-1}<\frac{1}{x_{n}-1}-1\\    \forall j \in \mN,\frac{1}{x_{j+k+1}-1} \le \frac{1}{x_{k+1}-1}-j\end{gather}
取$j>\frac{1}{x_{k+1}-1}$,则$\frac{1}{x_{j+k+1}-1}<0,x_{j+k+1}<1$,矛盾
故对一切$k \in \mN,0<x_k<1$
\begin{gather}    1-x_n>\frac{1}{x_{n+1}}-1=\frac{1-x_{n+1}}{x_{n+1}}>0\\    \frac{1}{1-x_n}<\frac{x_{n+1}}{1-x_{n+1}}=\frac{1}{1-x_{n+1}}-1,\frac{1}{1-x_{n+1}}>\frac{1}{1-x_n}+1\\    \frac{1}{1-x_n}>\frac{1}{1-x_1}+n-1>n\\    1-\frac{1}{n}<x_n<1\end{gather}

求最大的常数 $M$, 使得对任意一个满足如下条 件的无穷实数列 $\left\{a_n\right\}, n=0,1,2, \ldots$, 以及任 意 $n \geq 0$, 均有 $\frac{a_{n+1}}{a_n}>M$ :
(1)$a_0=1, a_1=3$;
(2)$a_0+a_1+\ldots+a_{n-1} \geq 3 a_n-a_{n+1}$.

解:取$a_n=(n+2)2^{n-1}$,则满足全部条件.
此时,$\frac{a_{n+1}}{a_n}=\frac{2(n+3)}{n+2}>M$恒成立.
取$n \to +\infty,M \le 2$
下面证明$M=2$是复合题意的:
令$S_n=a_0+a_1+a_2+\dots+a_n$,则原式化为\[    S_{n-1} \ge 3(S_n-S_{n-1})-(S_{n+1}-S_n)    \]
可得\[    S_{n+1}-2S_n \ge 2(S_n-2S_{n-1})    \]
于是有\[    S_{n}-2S_{n-1} \ge 2^{n-1}(S_1-2S_0)=2^n    \]
容易得到$S_n$递增,$a_n>0$,且\[    a_{n+1}-2a_n \ge a_n-(a_0+a_1+\dots+a_{n-1})=S_n-2S_{n-1}>0    \]
即\[    \frac{a_{n+1}}{a_n}>2    \]
    综上,$M$的最大值是2