在三角形 $A B C$ 中, $A B>A C, I$ 是内心, $A M$ 是中线. 设过 $I$ 且与 $B C$ 垂直的直线与 $A M$ 交于点 $L, I$ 关于点 $A$ 的对称点为 $J$. 证明: $\angle A B J=\angle L B I$.
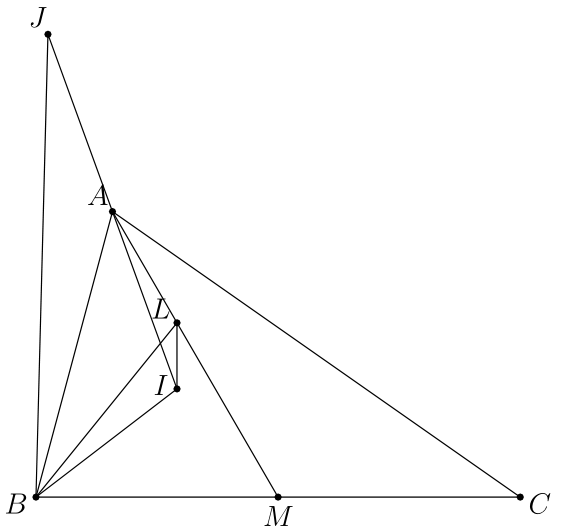
证明:
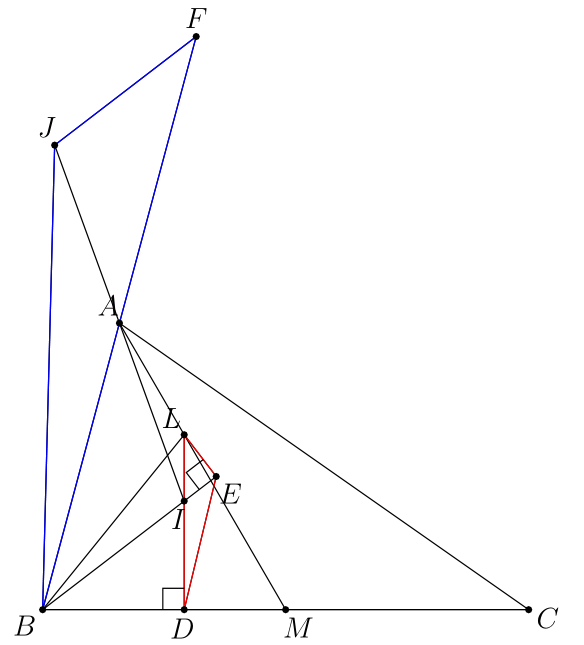
作$ID \perp BC$于$D$,$LE \perp BI$于$E$,延长$BA$至$F$,使得$AF=AB$
则$LBDE$共圆,$\angle LBI=\angle LDE$;$JFIB$是平行四边形.
由平行四边形及正弦定理 \begin{gather} \frac{FJ}{FB}=\frac{IB}{2AB}\\ =\frac{\sin\frac{A}{2}}{2\sin(90^\circ+\frac{C}{2})}=\frac{\sin\frac{A}{2}}{2\cos\frac{C}{2}} \end{gather}
显然$$\frac{LE}{LD}=\frac{LI \cos\frac{B}{2}}{LD}=\frac{LI}{LD}\cos\frac{B}{2}$$
记$BC$边上的高为$h$,外接圆半径$R$,由面积关系 \begin{gather} \frac{LI}{LD} =\frac{[AIM]}{[ADM]}=\frac{\frac{1}{2}([AIC]-[AIB])}{\frac{1}{2}([ADC]-[ADB])}\\ =\frac{\frac{r}{2}(b-c)}{\frac{h}{2}(DC-DB)}=\frac{\frac{r}{2}(b-c)}{\frac{h}{2}(b-c)}\\ =\frac{r}{h}=\frac{4R\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}}{2R\sin B \sin C} =\frac{\sin\frac{A}{2}}{2\cos\frac{B}{2}\cos\frac{C}{2}} \end{gather}
故 \[ \frac{LE}{LD}=\frac{LI \cos\frac{B}{2}}{LD}=\frac{LI}{LD}\cos\frac{B}{2}=\frac{\sin\frac{A}{2}}{2\cos\frac{C}{2}}=\frac{FJ}{FB} \]
结合$\angle DLE=\angle DBE=\frac{B}{2}=\angle BFJ$,故$\triangle DLE \sim \triangle BFJ$
有$\angle FBJ=\angle LDE=\angle LBE$,即$\angle ABJ=\angle LBI$
