上周学生问了我这样一个离心率问题
如图,椭圆的焦点$F_1$、$F_2$,椭圆上三点$A$、$B$、$C$满足:$F_1 \in AB,F_2 \in AC$.如果$\ds AF_2:F_2C=3:2,BF_2 \perp AC$.求椭圆的离心率.
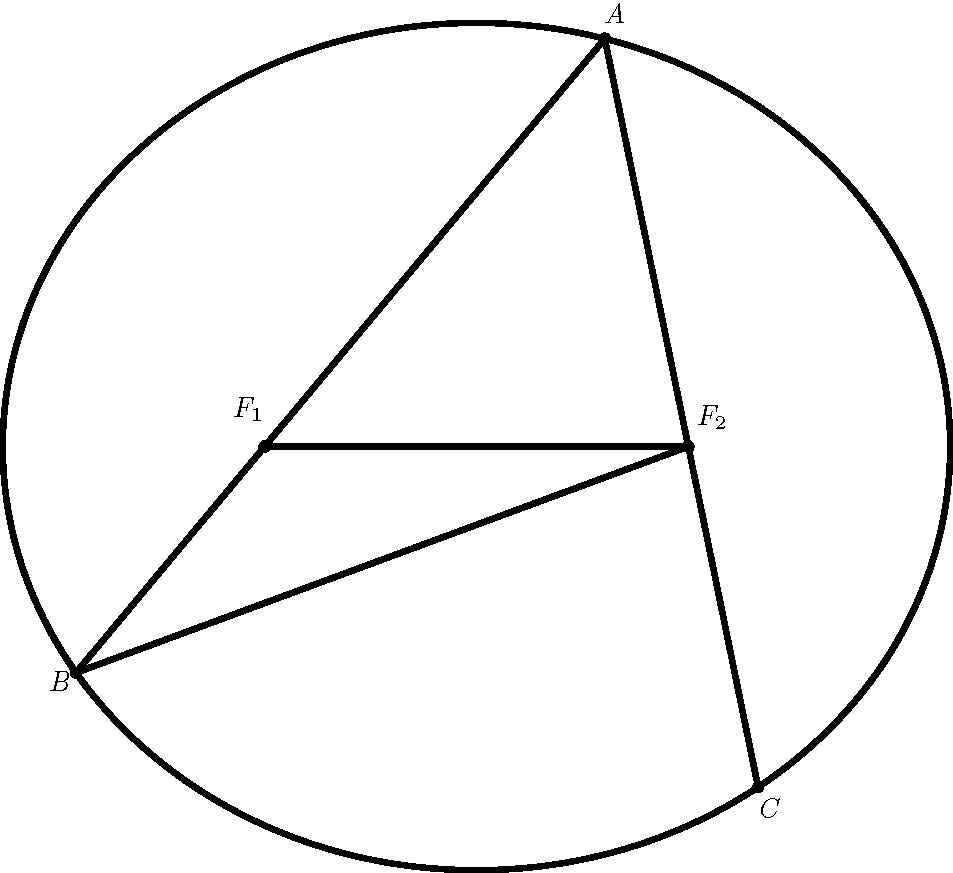
我当时给的解答是下面这样的:
设$AF_1=1,BF_1=x$,
则$\ds AF_2=(1+x)\cos A,BF_2=(1+x)\sin A$,
比例可得$\ds CF_2=\frac{2}{3}AF_2=\frac{2}{3}(1+x)\cos A$
考虑到椭圆定义,可得$AF_1+AF_2=BF_1+BF_2$,也就是\[ AF_1-BF_1=BF_2-AF_2,1-x=(1+x)(\sin A-\cos A)\]
两个变量,所以还需要建立一个方程才能解.这也是本题的主要矛盾.
下面这种做法需要用到椭圆极坐标方程得到的一个结论:过焦点的弦被焦点分割的两部分,它们的倒数和是常数.
对于本题来说就是:$\ds \frac{1}{AF_1}+\frac{1}{BF_1}=\frac{1}{AF_2}+\frac{1}{CF_2}$,等于某个公共常数(只与椭圆自身有关) 那么就可以建立第二个方程:\[ 1+\frac{1}{x}=\frac{1}{AF_2}+\frac{1}{CF_2}=\frac{1}{(x+1)\cos A} \cdot \frac{5}{2}\]
两个方程整理如下\[ \frac{1-x}{1+x}=\sin A-\cos A, \frac{(1+x)^2}{x}=\frac{5}{2\cos A}\]
注意到\[ \frac{4x}{(1+x)^2}=1-(\frac{1-x}{1+x})^2=1-(\sin A-\cos A)^2=2\sin A\cos A\]
和第二个式子相乘可得$\ds 4=5\sin A,\sin A=\frac{4}{5},\cos A=\frac{3}{5}$,
进而$\ds x=\frac{2}{3},AF_2=1,F_1F_2=\sqrt{1+1-2\cos A}=\frac{2}{\sqrt{5}}$
从而离心率\[ e=\frac{F_1F_2}{AF_1+AF_2}=\frac{\sqrt{5}}{5}\]
后来他们说拿给高三的学生做,做法也只有更复杂的,需要解四次方程之类的.(这个做法如果硬解也不容易,只是是用来恒等变形直接消元处理解方程才变得简单)
不知是否有更简单的做法
