锐角三角形$ABC$中,$D,E,F$为$BC,AC,AB$中点,$X,Y$为$D$在$AB$,$AC$上垂足,过$F$且与$XY$平行的直线与$DY$交于$P$。求证:$AD \perp EP$。
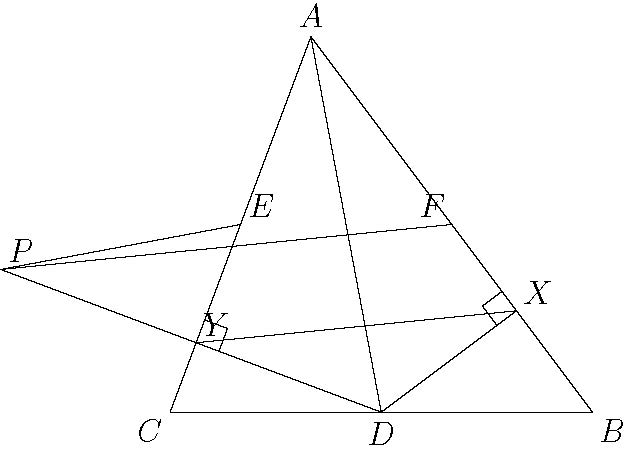
需要知道面积与定比分点的公式
注意到$AD \perp EP \iff$ $E$是$\triangle APD$垂心
\begin{gather} AD \perp EP \iff AP \perp DE \iff AP //XD \\ \iff [PDX]=[ADX] \iff [FYX]+[DYX]=[ADX] \\ \iff \frac{1}{2}([XAY]-[XBY])+\frac{1}{2}([BXY]+[CXY])=[ADX]\\ \iff \frac{1}{2}([XAY]+[XCY])=[ADX]\end{gather}考虑到\[ [XAY]+[XCY]=[ACX]=2[ADX] \]结论显然成立
