已知$\triangle ABC$的内角满足$\sin A+2\sin B=2\sin C$,求$\ds \frac{1}{\sin A}+\frac{1}{\sin B}-\frac{1}{\sin C}$的最小值

解法1:
使用内切圆换元,面积$s$\begin{gather}a=y+z, b=z+x, c=x+y  \\a=2(c-b) \Rightarrow y+z=2(y-z), y=3 z  \\s^2=x y z(x+y+z)=3 x z^2(x+4 z) \\\frac{1}{\sin A}+\frac{1}{\sin B}-\frac{1}{\sin c}=\frac{b c+c a-a b }{2 s}\\=\frac{x^2+4 x z+11 z^2}{2 \sqrt{3 x z^2(x+4 z)}} \geqslant \frac{2 \sqrt{11 z^2 \cdot\left(x^2+4 x z\right)}}{2 \sqrt{3 x z^2(x+4 z)}}=\frac{\sqrt{33}}{3}\end{gather}

解法2:
和差化积\begin{gather}    \frac{1}{2}= \frac{\sin C-\sin B}{\sin A}=\frac{2 \cos \frac{C+B}{2} \sin \frac{C-B}{2}}{2 \sin \frac{C+B}{2} \cos \frac{C+B}{2}}=\frac{\tan \frac{C}{2}-\tan \frac{B}{2}}{\tan \frac{C}{2}+\tan \frac{B}{2}} \\    \tan \frac{C}{2}= 3 \tan \frac{B}{2}, \tan \frac{B}{2}=x>0, \tan \frac{C}{2}=3 x\\    \tan \frac{A}{2} \tan \frac{B}{2}+\tan \frac{B}{2} \tan \frac{C}{2}+\tan \frac{C}{2} \tan \frac{A}{2}=1 \Rightarrow  \tan \frac{A}{2}=\frac{1-3 x^2}{4 x}>0\end{gather}
考虑万能公式\[    \frac{2}{\sin A}=\tan \frac{A}{2}+\cot \frac{A}{2}\]\begin{gather}    2\left(\frac{1}{\sin A}+\frac{1}{\sin B}-\frac{1}{\sin C}\right)=\frac{1-3 x^2}{4 x}+\frac{4 x}{1-3 x^2}+x+\frac{1}{x}-\left(3 x+\frac{1}{3x}\right) \\=  \frac{11}{12} \cdot \frac{1-3 x^2}{x}+4 \cdot \frac{x}{1-3 x^2} \geqslant 2 \sqrt{\frac{11}{12} \times 4}=2 \cdot \frac{\sqrt{33}}{3}\\\left(\frac{1}{\sin A}+\frac{1}{\sin B}-\frac{1}{\sin C}\right) \ge \frac{\sqrt{33}}{3}\end{gather}

对于一个正$n$边形,各边斜率均存在且分别为$k_j,j=1,2,\dots,n$,如果某边的倾斜角为$\theta$,化简$\ds A_n=\sum_{j=1}^n k_j\sum_{j=1}^n \frac{1}{k_j}$.

昨晚睡前在QQ群看到的一个讨论,原题是$n=5$,推广到$n$.和两年前写的下面这篇”从高考题到巴塞尔问题”关联比较大,如果没有接触过此类问题,可以从下面的文章开始阅读.

从高考题到巴塞尔问题

下面先证明一个引理:\[    F_n(\theta)=\sum_{j=1}^n \tan(\theta+\frac{j\pi}{n})=\begin{cases}        n\tan n\theta & 2 \nmid n\\        -n\cot n\theta & 2 | n    \end{cases}\]
证明:
考虑$x\in \{\theta+\frac{j\pi}{n} |j=1,2,\dots,n\}$的共同之处:$\tan nx=\tan n\theta$
且显然所有$\tan x$是互不相同的
考虑棣莫弗公式\[    \cos nx+\mi \sin nx=(\cos x+ \mi \sin x)^n\]
如果$n=2k+1$是奇数,比较实部虚部可得\begin{gather}    \tan n\theta=\tan nx=\frac{\sin nx}{\cos nx}\\    =\frac{C_{2k+1}^{2k+1}(-1)^k \sin^{2k+1} x+\dots}{C_{2k+1}^{2k}(-1)^k \cos x\sin^{2k} x+\dots}    =\frac{C_{2k+1}^{2k+1}(-1)^k \tan^{2k+1} x+\dots}{C_{2k+1}^{2k}(-1)^k \tan^{2k} x+\dots}\\    C_{2k+1}^{2k+1}(-1)^k \tan^{2k+1} x – \tan (2k+1)\theta \cdot C_{2k+1}^{2k}(-1)^k \tan^{2k} x+\dots=0\end{gather}从而$\tan(\theta+\frac{j\pi}{n})$是如下关于$y$的$2k+1$次方程的$2k+1$个不同根\[    C_{2k+1}^{2k+1}(-1)^k y^{2k+1} – \tan (2k+1)\theta \cdot C_{2k+1}^{2k}(-1)^k y^{2k}+\dots=0\]
韦达定理可得这些根的和\[    F_n(\theta)=-\frac{- \tan (2k+1)\theta \cdot C_{2k+1}^{2k}(-1)^k}{C_{2k+1}^{2k+1}(-1)^k} =(2k+1)\tan (2k+1)\theta=n\tan n\theta\]
如果$n=2k$是偶数,那么按照同样的操作同理可得$\tan(\theta+\frac{j\pi}{n})$是如下关于$y$的$2k$次方程的$2k$个不同根\[    C_{2k}^{2k} (-1)^k y^{2k} – \cot 2k \theta \cdot C_{2k}^{2k-1}(-1)^{k-1} y^{2k-1}+\dots=0\]
韦达定理可得\[    F_n(\theta)=-\frac{- \cot 2k \theta \cdot C_{2k}^{2k-1}(-1)^{k-1}}{C_{2k}^{2k} (-1)^k} =-2k\cot 2k\theta=-n\cot n\theta\]
综上可知\[    F_n(\theta)=\sum_{j=1}^n \tan(\theta+\frac{j\pi}{n})=\begin{cases}        n\tan n\theta & 2 \nmid n\\        -n\cot n\theta & 2 | n    \end{cases}\]

接着证明原题:
不妨设第$j$边倾斜角为$x_j=\theta+\frac{2j\pi}{n}$,(不管倾斜角$[0,\pi)$的取值范围,求正切以后无影响)\[    f_n(\theta)=\sum_{j=1}^n \tan(\theta+\frac{2j\pi}{n})\]
则\[    \sum_{j=1}^n \cot(\theta+\frac{2j\pi}{n})=\sum_{j=1}^n \tan(\frac{\pi}{2}-\theta-\frac{2j\pi}{n})=f_n(\frac{\pi}{2}-\theta)\]
待求式即为$A_n=f_n(\theta)f_n(\frac{\pi}{2}-\theta)$
若$n=2k+1$是奇数,则易得任意两个边倾斜角的差都不是$\pi$的整数倍,所以求正切后互不相同,是$\theta+\frac{j\pi}{n}$的重新排列
亦即$f_n(\theta)=F_n(\theta)$
\[    f_n(\frac{\pi}{2}-\theta)=n \tan n(\frac{\pi}{2}-\theta)=n \tan (k\pi+\frac{\pi}{2}-n\theta)=n \cot n\theta\]
于是待求为\[    A_n=f_n(\theta)f_n(\frac{\pi}{2}-\theta)=\left( n\tan n\theta \right) \left( n \cot n\theta \right)=n^2\]
若$n=2k$是偶数,则$x_1,x_2,\dots,x_k$的正切刚好取遍$\tan(\theta+\frac{j\pi}{k}),j=1,2,\dots,k$,而$\tan x_{k+j}=\tan x_j$
所以$f_{2k}(\theta)=2F_k(\theta),f_{2k}(\frac{\pi}{2}-\theta)=2F_k(\frac{\pi}{2}-\theta)$,待求式为\[    A_n=f_{2k}(\theta) f_{2k}(\frac{\pi}{2}-\theta)=4F_k(\theta)F_{k}(\frac{\pi}{2}-\theta)\]
如果$k$是奇数,如上可得\[    A_n=4k^2=n^2    \]
如果$k=2m$是偶数,那么$n=4m$\[    A_n=4F_{2m}(\theta)F_{2m}(\frac{\pi}{2}-\theta)=4 \cdot (-2m\cot 2m\theta) \cdot (-2m \cot 2m(\frac{\pi}{2}-\theta))=-n^2\cot^2\frac{n\theta}{2}\]

综上可得\[    A_n=\begin{cases}        -n^2\cot^2\frac{n\theta}{2} & 4|n\\        n^2 & else    \end{cases}\]

设 $H, O$ 分别为非等边锐角三角形 $A B C$ 的垂心和外心, 设 $C$ 关于直线 $A B$ 的对称点为 $C^{\prime}, B C^{\prime} \cap A O=L$, 过 $B$ 作关于 $A O$ 的平行线交直线 $A C$ 于点 $Z$, 求证: $\angle L Z B=\angle C Z H$.

解析:容易得$\angle ZBL=90^\circ+A$,结合$\angle HCA=90^\circ-A$,所以我们可以尝试强行构造相似三角形,用SAS的方式证明相似从而得等角.具体如下
    以$H$为圆心,$HC$为半径作圆,交$ZC$于不同于$C$的点$D$,则$\angle ZDH=\angle ZBL=90^\circ+A$
    我们只需证明$\frac{DZ}{DH}=\frac{BZ}{BL}$即可证明原题
    \begin{align}        \frac{BZ}{BL}&=\frac{BZ}{BA}\frac{BA}{BL}\\        &=\frac{\sin A}{\cos B}\frac{\cos A}{\cos C}    \end{align}
    另一方面,考虑$CD=2CH \cdot \cos\angle ACH=2CH\sin A$,以及    \begin{align}        \frac{CZ}{CH}&=\frac{CA+AZ}{AB}\frac{AB}{CH}\\        &=(\frac{CA}{AB}+\frac{AZ}{AB})\frac{AB}{CH}\\        &=(\frac{\sin B}{\sin C}+\frac{\cos C}{\cos B})\frac{\sin C}{\cos C}\\        &=\frac{\sin 2B+\sin 2C}{2\cos B \cos C}\\        &=\frac{\sin(B+C)\cos(B-C)}{\cos B \cos C}\\        &=\sin A \frac{\cos(B-C)}{\cos B \cos C}    \end{align}
    所以    \begin{align}        \frac{DZ}{DH}&=\frac{CZ-2CH\sin A}{DH}=\frac{CZ}{CH}-2\sin A\\        &=\sin A \frac{\cos(B-C)}{\cos B \cos C}-2\sin A\\        &=\sin A \frac{\cos(B-C)-2\cos B \cos C}{\cos B \cos C}\\        &=\sin A \frac{-\cos(B+C)}{\cos B \cos C}\\        &=\frac{\sin A \cos A}{\cos B \cos C}=\frac{BZ}{BL}    \end{align}
    证毕.

学校发的小题专练里的题目
12. 已知函数 $f(x)=2 \sin (\omega x+\varphi)+h$ 的最小正周期为 $\pi$, 若 $|f(x)|$ 在 $\left[0, \frac{\pi}{4}\right]$ 上的最大值为 $M$, 则 $M$ 的最小值为$\tk$

解:考虑$f(0)=2\sin\varphi +h,f(\frac{\pi}{8})=\sqrt{2}\sin\varphi+\sqrt{2}\cos\varphi+h,f(\frac{\pi}{4})=2\cos\varphi+h$
\begin{gather}    2M \ge |f(0)-f(\frac{\pi}{8})|=|(2-\sqrt{2})\sin\varphi-\sqrt{2}\cos\varphi|\\    2M \ge |f(\frac{\pi}{4})-f(\frac{\pi}{8})|=|(2-\sqrt{2})\cos\varphi-\sqrt{2}\sin\varphi|\\    (2M)^2+(2M)^2 \ge |(2-\sqrt{2})\sin\varphi-\sqrt{2}\cos\varphi|^2+|(2-\sqrt{2})\cos\varphi-\sqrt{2}\sin\varphi|^2\\    =8-4\sqrt{2}-(4\sqrt{2}-4)\sin 2\varphi \ge 12-8\sqrt{2}\\    M \ge \frac{2-\sqrt{2}}{2}\end{gather}当$\varphi=\frac{3\pi}{4},h=-\frac{2+\sqrt{2}}{2}$取等

各位新年快乐~

2016山东文科高考题

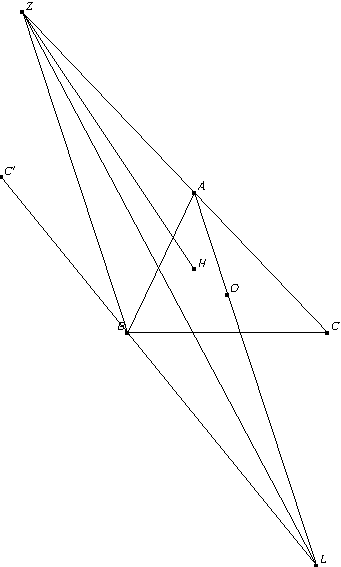
2016年山东省文科高考题第12是这样一个问题:
12. 观察下列等式:\[\begin{aligned}&\left(\sin \frac{\pi}{3}\right)^{-2}+\left(\sin \frac{2 \pi}{3}\right)^{-2}=\frac{4}{3} \times 1 \times 2 \\&\left(\sin \frac{\pi}{5}\right)^{-2}+\left(\sin \frac{2 \pi}{5}\right)^{-2}+\left(\sin \frac{3 \pi}{5}\right)^{-2}+\left(\sin \frac{4 \pi}{5}\right)^{-2}=\frac{4}{3} \times 2 \times 3 ; \\&\left(\sin \frac{\pi}{7}\right)^{-2}+\left(\sin \frac{2 \pi}{7}\right)^{-2}+\left(\sin \frac{3 \pi}{7}\right)^{-2}+\cdots+\left(\sin \frac{6 \pi}{7}\right)^{-2}=\frac{4}{3} \times 3 \times 4 ;\\&\left(\sin \frac{\pi}{9}\right)^{-2}+\left(\sin \frac{2 \pi}{9}\right)^{-2}+\left(\sin \frac{3 \pi}{9}\right)^{-2}+\cdots+\left(\sin \frac{8 \pi}{9}\right)^{-2}=\frac{4}{3} \times 4 \times 5 ; \end{aligned}\]
照此规律, $\ds \left(\sin \frac{\pi}{2 m+1}\right)^{-2}+\left(\sin \frac{2 \pi}{2 m+1}\right)^{-2}+\left(\sin \frac{3 \pi}{2 m+1}\right)^{-2}+\cdots+ \left(\sin \frac{2 m \pi}{2 m+1}\right)^{-2}=\tk$

此题是一个填空题,仅仅猜想的话是很容易观察出结果的$\ds \frac{4m(m+1)}{3}$.但它实际有相当深刻的背景.真的去证明的话需要用到一系列高考以外的知识.

(I).基础知识:
首先我们需要知道棣莫弗公式:
$\mi$是虚数单位,则
\[    \forall m \in \mN:(\cos x+\mi\sin x)^m=\cos mx+i\sin mx\]
这可以用归纳法证明.

还需知道一个基本三角函数不等式\[    \forall x \in (0,\frac{\pi}{2}),0<\sin x<x<\tan x\]

还需要知道多元韦达定理的推论:
方程 $\ds \sum_{k=0}^{n} a_k x^k=0(a_n a_0 \ne 0)$ 的所有根的倒数和为 $\ds -\frac{a_1}{a_0}$

(II).然后我们需要进行一步转化,利用$\sin^{-2} x=\tan^{-2} x+1$及正弦函数的对称性将原式化为\[    \sum_{k=1}^{2m} \sin^{-2}\frac{k\pi}{2m+1}=2\sum_{k=1}^{m} (\tan^{-2}\frac{k\pi}{2m+1}+1)\]

(III).构建以$\ds \tan^2 \frac{k\pi}{2m+1},k=1,2,\dots,m$为根的方程,使用韦达定理求和.
\begin{gather}    n=2m+1,m \in \mathbf{N}^*\\    \tan nx=0 \Longleftrightarrow \sin nx=0\\    \Longleftrightarrow Im((\cos x+\mathbf{i} \sin x)^n)=0\\    \Longleftrightarrow C_n^1 \cdot \cos^{n-1} x \cdot \sin x-C_n^3 \cdot \cos^{n-3} x \cdot \sin^3 x+\ldots=0\end{gather}
后面的项我们不关心所以直接省略掉,前两项是会用到的
\[    \Longleftrightarrow C_n^1 \tan x-C_n^3 \tan^3 x+\ldots=0\]从而$\ds \tan\frac{k\pi}{2m+1},|k| \le m$是 $n$ 次方程 $C_n^1 x-C_n^3 x^3+\ldots=0$ 的全部根
由于方程只有奇数幂,扣掉0根,扣掉负根,可得
$\ds \tan^2\frac{k\pi}{2m+1},1 \le k \le m$是$m$次方程 $C_n^1 -C_n^3 x+\ldots=0$的全部根
从而由韦达定理\[    \sum_{k=1}^{m} \frac{1}{\tan^2\frac{k\pi}{2m+1}}=\frac{C_n^3}{C_n^1}=\frac{(n-1)(n-2)}{6}=\frac{2m^2-m}{3}\]
从而得到题目中的待求式\[    \sum_{k=1}^{2m} \sin^{-2}\frac{k\pi}{2m+1}=2\sum_{k=1}^{m} (\tan^{-2}\frac{k\pi}{2m+1}+1)=2(\frac{2m^2-m}{3}+m)=\frac{4m(m+1)}{3}\]

这样我们就得到了这道高考题的证明.

巴塞尔问题

说完这个高考题的证明,我们接着介绍历史上著名的巴塞尔问题,也就是平方数的倒数和究竟是多少?

巴塞尔问题是一个著名的数论问题，这个问题首先由皮耶特罗·门戈利在1644年提出，由莱昂哈德·欧拉在1735年解决。由于这个问题难倒了以前许多的数学家，欧拉一解出这个问题马上就出名了，当时他二十八岁。欧拉把这个问题作了一番推广，他的想法后来被黎曼在1859年的论文《论小于给定大数的素数个数》（On the Number of Primes Less Than a Given Magnitude）中所采用，论文中定义了黎曼$\zeta $函数，并证明了它的一些基本的性质。这个问题是以瑞士的第三大城市巴塞尔命名的，它是欧拉和伯努利家族的家乡。
这个问题是精确计算所有平方数的倒数的和，也就是以下级数的和：
${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=\lim _{n\to +\infty }\left({\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}\right)}$
这个级数的和大约等于1.644934（OEIS中的数列A013661）。巴塞尔问题是寻找这个数的准确值，并证明它是正确的。欧拉发现准确值是$\frac{\pi^2}{6}$，并在1735年公布；彼时他的证明还不是十分严密，真正严密的证明在1741年给出。

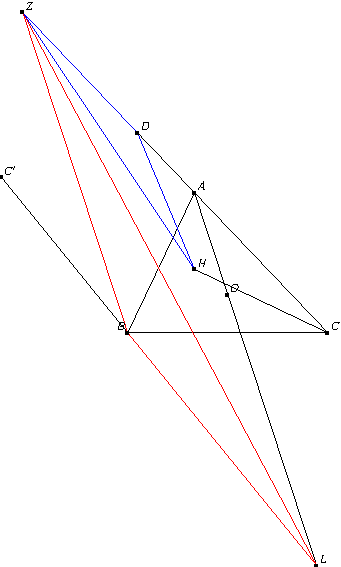
我们下面会指出,这道高考题与巴塞尔问题有着内在联系,实质上它稍微处理一下就可以解决巴塞尔问题.

我们利用上面的中间结论\[    \sum_{k=1}^{m} \cot^2\frac{k\pi}{2m+1}=\frac{2m^2-m}{3},\sum_{k=1}^{m} \frac{1}{\sin^2 \frac{k\pi}{2m+1}}=\frac{2m^2+2m}{3}\]
使用基本的三角不等式,我们知道\[    0<\cot^2 x<\frac{1}{x^2}<\frac{1}{\sin^2 x}, \forall x \in (0,\frac{\pi}{2})\]
从而\[    0<\cot^2 \frac{k\pi}{2m+1}<\frac{(2m+1)^2}{k^2 \pi^2}<\frac{1}{\sin^2 \frac{k\pi}{2m+1}},k=1,2,\dots,m\]
我们将所有的不等式加起来,两边都是可以求和的,从而得到\[    \frac{m(2m-1)}{3}<\frac{(2m+1)^2}{\pi^2}(1+\frac{1}{2^2}+\dots+\frac{1}{m^2})<\frac{2m(m+1)}{3}\]
从而\[    \frac{\pi^2}{6}\frac{2m(2m-1)}{(2m+1)^2}<1+\frac{1}{2^2}+\dots+\frac{1}{m^2}<\frac{\pi^2}{6}\frac{4m(m+1)}{(2m+1)^2}\]
令$m \to +\infty$显然两边都以$\ds \frac{\pi^2}{6}$为极限
所以\[    \sum_{k=1}^{+\infty} \frac{1}{k^2}=\frac{\pi^2}{6}\]

这样就解决了历史上著名的巴塞尔问题.

附注:
3Blue1Brown 做过一次关于巴塞尔问题的视频,也值得一看
https://www.bilibili.com/video/av20400157/

练习题:
求$\ds\tan^6 \frac{\pi}{9}+\tan^6 \frac{2\pi}{9}+\tan^6 \frac{4\pi}{9}$
答案:33273

若函数$f(x)=|a\sin x+b \cos x-1|+|b \sin x-a \cos x|,(a,b \in \mr)$的最大值为11,则$a^2+b^2=\tk$

本题需要利用基本的绝对值恒等式:$|a|+|b|=\max\{|a+b|,|a-b|\}$

\begin{gather}    f(x)=\max\{|(a+b)\sin x+(b-a) \cos x-1|,|(a-b)\sin x +(a+b)\cos x-1|\}\\    \le \sqrt{(a+b)^2+(a-b)^2}+1    =\sqrt{2(a^2+b^2)}+1\end{gather}

且只要$(a-b)\sin x +(a+b)\cos x=-\sqrt{2(a^2+b^2)}$就能取到等号,而根据辅助角公式我们知道这总是可以做到的
所以$\max f(x)=\sqrt{2(a^2+b^2)}+1=11$

$a^2+b^2=50$

    \[    \sin nx=2^{n-1} \prod_{k=0}^{n-1} \sin(x+\frac{k\pi}{n})    \]

    令$\displaystyle \alpha=\frac{\pi}{n}$    

\begin{gather*}    \exp(2nx\mi)-1    =\prod_{k=0}^{n-1}(\exp(2x\mi)-\exp(2k\alpha \mi))\\    =\prod_{k=0}^{n-1} [\exp(x+k\alpha)\mi \cdot 2\mi \cdot \sin(x-k\alpha)] \\   =\prod_{k=0}^{n-1}\exp(nx\mi+\frac{n-1}{2}\pi\mi) \cdot (2\mi)^n \cdot \prod_{k=0}^{n-1}\sin(x-k\alpha)\\    =2^n \cdot \exp(\frac{n\pi}{2}\mi) \cdot \exp(nx\mi) \cdot \exp(\frac{n-1}{2}\pi\mi) \cdot \prod_{k=0}^{n-1}\sin(x-k\alpha)\\    =2^n \cdot \exp(nx\mi) \cdot \mi^{2n-1} \cdot \prod_{k=0}^{n-1}\sin(x-k\alpha)    \end{gather*}
    因此可得    \begin{gather*}    \exp(nx\mi)-\exp(-nx\mi)    =2^n \cdot \mi^{2n-1} \cdot \prod_{k=0}^{n-1}\sin(x-k\alpha)    =-2^n \cdot \mi \cdot \prod_{k=0}^{n-1}\sin(k\alpha-x)\\    =-2^n \cdot \mi \cdot \prod_{k=0}^{n-1}\sin(x+\frac{n-k}{n}\pi)    =2^n \cdot \mi \cdot \prod_{k=0}^{n-1}\sin(x+\frac{k\pi}{n})    \end{gather*}

    再利用$\exp(nx\mi)-\exp(-nx\mi)-2\mi \sin nx$即得证.

如果只是需要绝对值的话,对$\exp(2nx\mi)-1=\prod_{k=0}^{n-1}(\exp(2x\mi)-\exp(2k\alpha \mi))$两边取模即可,这个对于计算具体的数字会有用.但如果计算一般的式子还是需要上面的做法

设$m,n$是两个正整数且$m>n$,证明:$$\sum_{k=1}^{m-1} \sin^{2n} \frac{k\pi}{m}=\frac{mC_{2n}^n}{2^{2n}}$$

证明:
令$z=\exp(\frac{\pi}{m}i)$,则$|z|=1,z^{2m}=1$\[(z-\frac{1}{z})^{2n}=\sum_{k=0}^{2n} C_{2n}^k z^{2n-k}(-\frac{1}{z})^k=\sum_{k=0}^{2n}(-1)^k C_{2n}^k z^{2n-2k}=\sum_{j=-n}^{n}(-1)^{n-j} C_{2n}^{n-j} z^{2j}\]

接下来,用$z^r,r=0,1,2,\ldots,m-1$替换上式的$z$,并对所有可能值求和\begin{gather*}\sum_{r=0}^{m-1} (z^r-\frac{1}{z^r})^{2n}=\sum_{j=-n}^{n} (-1)^{n-j} C_{2n}^{n-j}(\sum_{r=0}^{m-1} z^{2rj})\end{gather*}
由于$|2j| \le 2n<2m$,故当$j \ne 0,z^{2j} \ne 1$,此时总有\[\sum_{r=0}^{m-1} z^{2rj}=\frac{z^{2mj}-1}{z^{2j}-1}=0\]

从而\[\sum_{r=0}^{m-1} (z^r-\frac{1}{z^r})^{2n}=(-1)^{n} C_{2n}^{n} \cdot m\]
又有\[\sum_{r=0}^{m-1} (z^r-\frac{1}{z^r})^{2n}=\sum_{r=0}^{m-1} (2i\sin\frac{r\pi}{m})^{2n}=(-1)^n \cdot 2^{2n} \sum_{r=0}^{m-1} \sin^{2n}\frac{r\pi}{m}\]
故\[(-1)^{n} C_{2n}^{n} \cdot m=(-1)^n \cdot 2^{2n} \sum_{r=0}^{m-1} \sin^{2n}\frac{r\pi}{m}\]
即\[\sum_{r=1}^{m-1} \sin^{2n}\frac{r\pi}{m}=\sum_{r=0}^{m-1} \sin^{2n}\frac{r\pi}{m}=\frac{m C_{2n}^n}{2^{2n}}\]